1. 서 론
2. 연구 방법
2.1 모형의 특성
2.2 모형의 구축
2.3 하도지형의 전처리
3. 결과 및 고찰
3.1 모형의 검보정
3.2 예측모의
3.3 모형의 한계 및 개선사항
4. 결론 및 제언
1. 서 론
보는 하천에서 수위통제와 용수공급 등의 목적으로 설치되며 전반적으로 출구 높이가 고정된 고정보와 출구 면적이 조절 가능한 가동보로 구분된다. 이들 보에 흐르는 물의 특성은 수리학적으로 크게 월류 또는 오리피스 흐름으로 간주될 수 있다 (KICT 2011). 현재 4대강에는 16개의 다기능 보가 설치되어 있으며 홍수기에는 보 상류의 최대관리 상한수위를 설정하여 수위를 통제하고 있다. 또한 가동보의 수문개방을 통해 방류량을 조절하여 홍수기에 대처하고 있다. 평갈수기에는 최소 관리하한수위를 기반으로 가동보의 수문을 폐쇄하여 공급용수를 확보하는 이수적 기능을 수행하기도 한다.
보는 전술한 기능을 통해 이수와 치수에 긍정적인 영향을 미치기도 하며 유량변화와 유사차단으로 인해 하류부에서 수생물의 서식처 변화 및 수공구조물의 안정성에 영향을 주기도 한다. 특히, 유량과 유사이송의 변화는 수공구조물의 근처에서 세굴을 일으키기도 한다. 이를 위해 고정보와 가동보를 연계하는 다양한 운영방식을 수립하는 것이 일반적이며, 이때 보의 운영에 따른 하류부 수공구조물의 안정성을 검토하는 것이 무엇보다 중요하다고 판단된다 (Lee et al. 2014).
이러한 수공구조물의 안정성을 사전에 예측하고 분석하기위해 국내외적으로 많은 연구들이 수행되어왔다. Kim (2005)은 실제하천과 동일한 축척의 수리모형을 이용하여 수리구조물의 형태에 따라 변화되는 흐름특성을 실내실험을 통해 분석하였다. Yeo et al. (2005)은 보의 높이보다 수위가 높은 경우를 가정하여 실내실험을 수행 후, 수위-유량관계를 기존의 위어공식들과 비교하였다. Choi et al. (2006)은 수리모형실험을 통하여 유입구가 있는 가동보에 대해 보의 설치에 따른 수위상승효과를 분석하였고 이와 더불어 가동보 각도 변화에 대한 상류측 수위변동 및 저층수 유입구에 따른 수위변화 등에 대해서도 연구하였다. Han et al. (2013)은 인양식 수문의 개폐조건에 따른 하류부 흐름특성의 변화를 연구하기 위해 실내실험을 수행하였고 실험결과로 도출된 도수거리와 하상보호공 공식 (Bligh 공식)을 비교하였다. Watanabe et al. (2013) 은 고정된 오리피스에 다양한 첨두량의 홍수류를 발생시켜 유사이송 및 하상변동이 어떻게 발생하는지를 실내실험을 수행하여 분석하였다. Lee and Jang (2018)은 실내실험을 통해 가동보의 운영에 따른 하상경사 변화와 보 상류 퇴사과정에 대해 실내실험을 수행하여 수리학적인 발달과정을 분석하였다.
수치해석의 측면에서는 하천의 수리학적 조건과 수공구조물에 발생하는 세굴을 다루기도 했으며, 주로 정류상태의 최대유속에 의한 장기세굴심의 변화를 예측모의하였다 (Yoon et al. 2014). Murata et al. (2012)의 경우에는 1차원 및 3차원 흐름모형을 이용하여 홍수기의 유량변화와 보의 영향에 따른 흐름모의를 수행하였다. 여기서, 1차원 모형에서는 수위의 변화에 따라 오리피스 흐름과 월류를 구분하여 모의하였으며, 3차원 모형에서는 밀도함수를 이용하여 수위변화에 따른 셀 내부의 기체와 액체의 혼합비율을 적용하여 흐름률을 계산하였고 1차원 모형과 동일하게 오리피스와 월류를 동시에 고려하여 실제홍수량에 가까운 모의결과를 재현하였다. Lee et al. (2014, 2015)은 가동보의 운영을 고려하여 월류 및 오리피스의 흐름을 모형에 적용한 1차원 “통합하천수리해석모형”을 개발하였고 이를 개선하여 실제 하류부 구조물의 안정성을 수치모형을 통해 예측분석 하였다. Kang and Jang (2020)의 경우 2차원 흐름모형에 흐름률통제함수 모듈을 시범적으로 적용하여, 가변적인 수문개방률에 따른 보 하류부의 흐름 및 지형응답에 대한 모의를 시도하였고, 이를 통해 수문의 개방률에 따른 흐름모의를 수치계산과정에서 직접적으로 적용할 수 있는 가능성을 제시하였다.
이처럼 많은 연구자들이 실내실험과 수치해석을 통해 보의 영향에 따른 흐름변화와 유사이송 및 수리구조물의 안정성을 연구해왔으나, 더 다양하고 복잡한 하천환경을 통제하고 예측하기 위해서는 더욱 폭 넓고 세부적인 연구들과 예측도구들이 요구되고 있는 실정이다.
본 연구는 이러한 추세에 맞추어 보의 운영에 따른 흐름해석의 예측방법론을 위한 수치기법개발을 수행하고자 그에 대한 첫 단계로서 제방형보에 의한 자유형 월류흐름에 대한 수치해석실험을 수행하였다. 이를 위해 2차원 흐름모형인 Nays2DH를 이용하여 기존에 수행된 실험자료 (Hermann and Willi 1998)를 바탕으로 수치실험을 수행하여 비교검증하였다. 이 과정에서 위어의 형태로 인해 발생하는 불연속흐름을 보정하기 위해 본 연구에서 고안된 4점평균법을 이용하여 하도의 전처리 과정을 수행하였다. 이후에, 수문의 갯수를 고려한 월류흐름의 예측모의를 수행하여 결과를 비교분석하였다. 본 연구는 보의 운영에 따른 수문의 개방구성을 반영한 흐름특성을 수치해석적으로 예측할 수 있음을 보여주었으며 이는 추후의 보의 운영에 따른 흐름 및 유사이송 등을 고려하는 수리학적 연구의 기초자료가 될 것으로 기대된다.
2. 연구 방법
2.1 모형의 특성
2차원 모형은 천수방정식을 기반으로 하는 Nays2DH (Shimizu et al. 2012)를 활용했으며 여기서 본 모형은 실제하도의 곡선을 포착하기 위해 곡선좌표계 (generalized curvilinear coordinates)가 적용된다. Nays2DH의 지배방정식은 아래와 같다.
연속방정식:
| $$\frac\partial{\partial t}\left(\frac hJ\right)+\frac\partial{\partial\xi}\left(\frac{hU_\xi}J\right)+\frac\partial{\partial\eta}\left(\frac{hU_\eta}J\right)=0$$ | (1) |
운동량 방정식:
| $$C_f=\frac{gn^2}{h^{\displaystyle\frac13}}$$ | (4) |
여기서 주요 변수로는, ξ와 η는 각각 곡선좌표계의 성분; t는 시간; x와 y는 직교자표계 (Cartesian coordinate)의 성분; g는 중력가속도 (=9.81 m/s2); H는 수위 (m); h는 수심 (m); Dξ는 Dη 난류점성항; U는 유속성분; Cf는 하상전단응력; n은 Manning 계수; J는 자코비안변환 매개변수 (Transforming parameter of the Jacobian)이다. 세부적인 내용은 Shimizu et al. (2012)에 기술되어있다.
본 모형은 물의 흐름방향에 의존적으로 발생하는 하상전단응력을 계산하기 위해 시간에 대하여 음해법을 이용하고 있다. 또한 하상고의 형태가 완만한 곡선이 아닌 급변하는 첨예한 직선일 경우, 수치진동이 발생하기 쉽기 때문에 본 모형은 이를 저감하기 위해 흐름영역의 변화를 가상경계 (immersed boundary)기법 중의 하나인 Direct force (Mohd 1997)기법과 유사한 계산방식으로 유동에 따른 유속벡터의 재산정 과정을 수행한다. 우선은 본 모형은 압력은 격자내부에서, 유속은 격자의 경계면에서 계산되는 엇갈린 격자 (staggered grid)를 이용하고 있으며 연속방정식 (Eq. 1)에서 각 셀의 body force를 프아송 (Poisson)방정식에 기반하여 축차가속완화법 (successive over relaxation)으로 계산한다. 이후 계산된 body force를 운동량 방정식 (Eqs. 2 and 3)의 우변에 적용하여 유속벡터를 재산정한다. 그 다음에는 재산정된 유속벡터를 연속방정식 (Eq. 1)에 적용하여 body force를 재계산한다. 여기서, 모든 셀에 대한 body force의 입출량의 총합이 허용오차에 도달할 때까지 위 과정을 반복 계산한다.
이송항에 대해서는 시간과 공간적으로 양해법에 기반하는 3차정도의 TVD-MUSCL (Total variation diminishing-monotonic Upwind Scheme for Conservation Laws)기법을 활용하고 있으며 난류는 Zero 방정식 모형을 이용한다. 또한 병렬처리를 위해 OpenMP를 이용하여 계산 시간을 저감하고 있다.
2.2 모형의 구축
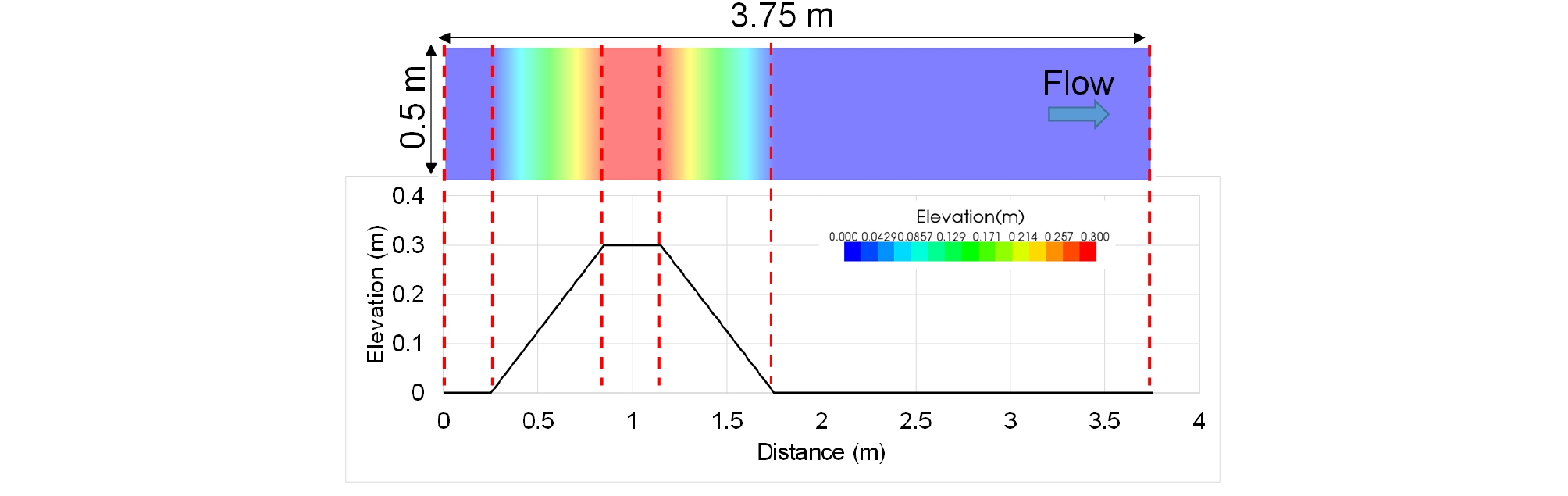
본 연구에서는 실내실험 (Hermann and Willi 1998)자료를 바탕으로 길이 3.75 m, 폭 0.5 m의 계산영역을 0.01 m × 0.01 m의 정방형 격자로 구축하였으며, 하도경사는 실내실험과 동일하게 수평으로 설정하고 상류단은 유량 (80 L/s), 하류단은 수심 (0.28 m)으로 경계조건을 설정하여 상류부의 수위가 충분히 정적평형 상태가 되는 120초 동안 모의를 수행하였다. 실내실험에서 구성된 위어는 불투수성으로 재질은 수로하상과 유사한 polyvinyl chloride이다. 따라서 Manning 계수는 실내실험자료에서 나타난 매끄러운 수로의 재질을 고려하여 n = 0.005, 0.01, 0.015의 예비계수를 선정하고 민감도 분석을 통해 모형의 정확성을 검증하였다. 위어의 마루폭은 0.5 m, 마루고는 0.3 m이며 종방향 위어 하부길이는 1.5 m (0.25 - 1.75 m 구간)로 하여 위어의 사면경사가 1 (수직) : 2 (수평)가 되도록 하였다.
2.3 하도지형의 전처리
본 연구에서는 위어마루에서 발생하는 불연속 흐름으로 야기된 한계류 계산의 오차를 보정하기 위하여 4점평균법을 고안하여 하도지형의 전처리를 수행하였다. 여기서, 4점평균법이란 프아송 방정식의 수치해법과 유사한 계산방식으로 이웃격자의 하상고도를 이용해 해당격자의 고도를 평균화하는 방법이다. 해당공식은 아래와 같이 표현된다.
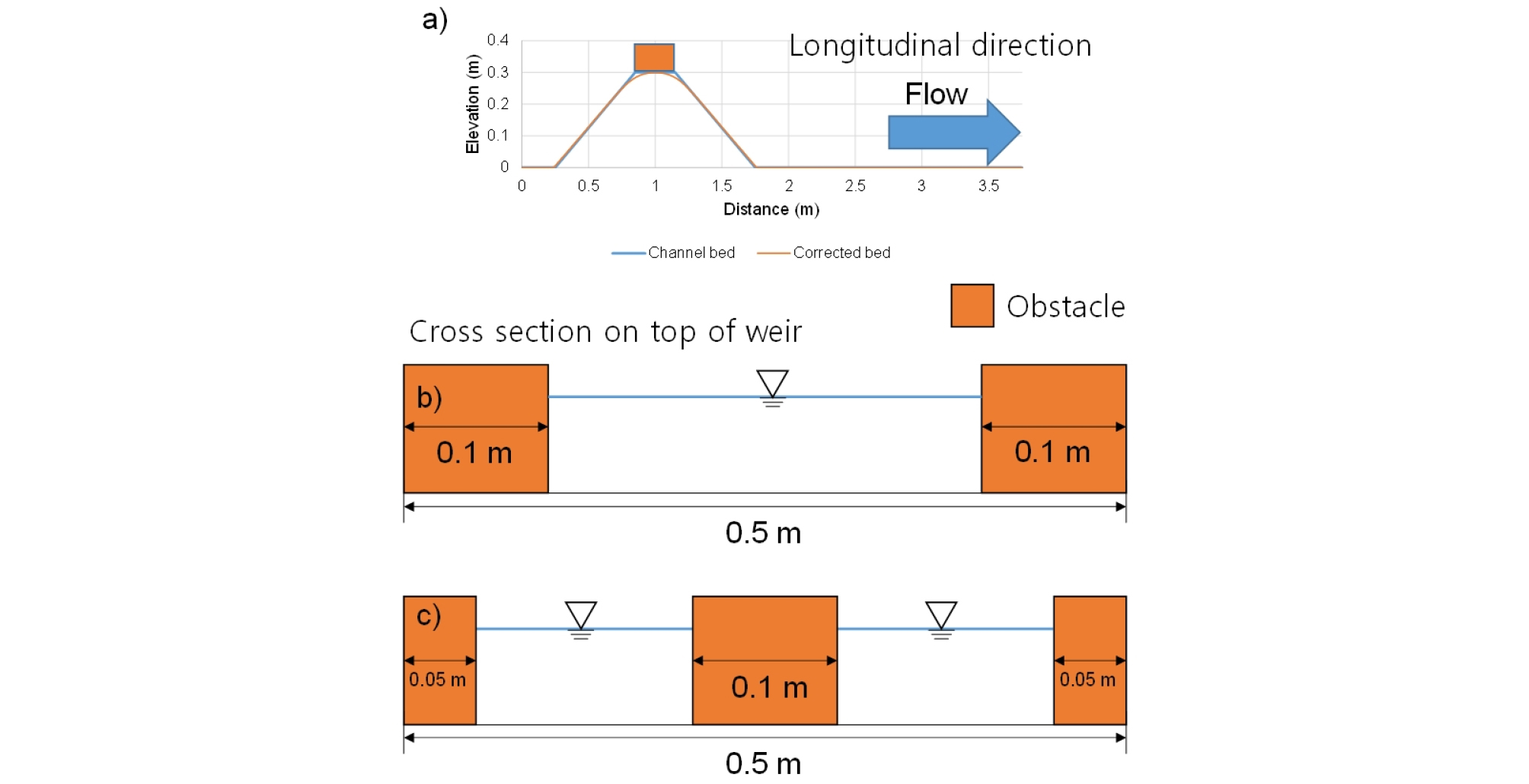
여기서 Zold, Znew는 각각 평균화 되기 전후의 하상고; i, j는 각각 계산격자의 종방향 및 횡방향 인덱스; top는 위어의 최고점으로 설정된 구간이다 (본 연구에서는 위어의 중앙부분 (1 m 구간)으로 설정함). Fig. 2는 임의로 선정한 Manning 계수 (n = 0.015)를 조건으로 모의된 결과이며, “EXP”는 실내실험, “Bed”는 재구성된 하상, “WL”은 수위, “0 - 150”은 반복횟수를 나타낸다. 4점평균법은 반복횟수에 따라 Fig. 2와 같이 위어를 완만한 곡선으로 재구성하게 되며, 반복횟수가 무한대에 가까워지면 위어는 삼각형 모양으로 재구성되어진다. 본 연구에서는 Fig. 2의 적색상자 구간에서 4점평균법을 150회 반복하여 재구성된 하도지형이 위어마루 부근에서 실험결과와 유사한 수위형태 (Fig. 2에서 WL150)를 보여준다고 판단하였고, 이를 이용하여 Manning 계수에 따라 수치모의 검보정을 수행한 후 모형의 정확도를 정량화 하였다. 검보정이후에는 보의 형상을 Fig. 2처럼 가정하여, 수문 갯수에 대한 흐름변화를 고려하여 예측모의를 수행하였다. 위어마루 (Fig. 3 (a))에 통수가 가능한 구간 외에는 모두 장애물로 고려하여 Fig. 3 (b), 3 (c)처럼 흐름이 통과하지 못하는 것으로 가정하였다.
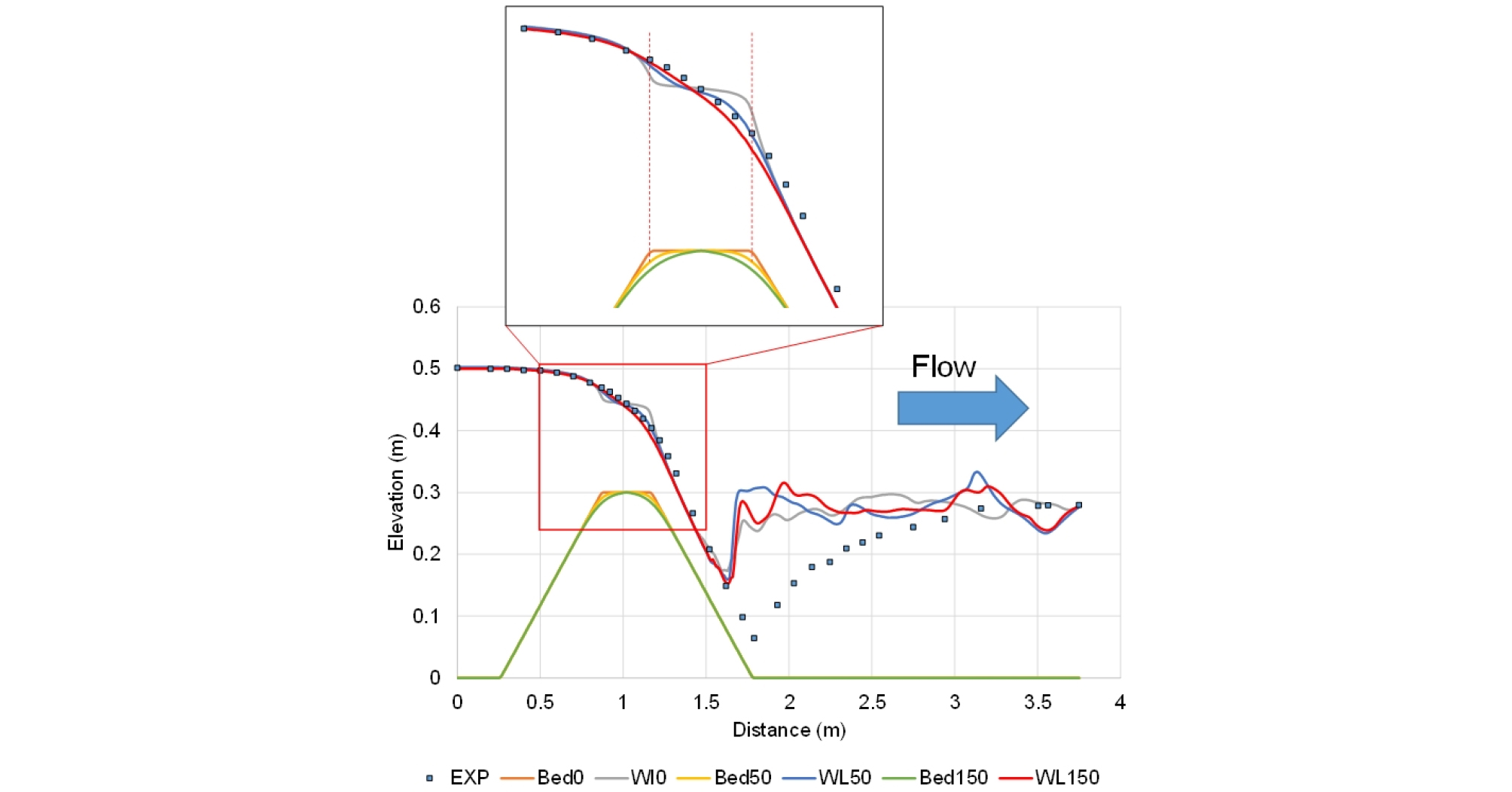
Fig. 2.
Simulation results depending on the iteration number of four-point averaging (EXP: gauged water level of Hermann and Willi (1998), Bed: channel bed, WL: water level, 0 - 150: the iteration number).
3. 결과 및 고찰
3.1 모형의 검보정
Fig. 4는 Manning 계수에 의한 수위변화를 나타낸다. 여기서, 계산된 수위는 보 상류의 수위가 충분히 평형을 이루어 변화가 나타나지 않는 30 s 부터 30 s 간격 (30 s 에서 120 s까지 총 4개)으로 모의 결과를 산출한 뒤 이를 앙상블 (ensemble)방식으로 평균화하였다. Fig. 4에서 “n”은 계산에서 고려된 Manning 계수를 의미하며 0.005, 0.01, 0.015 값에 의한 수위를 나타낸다. “EXP”는 실내실험자료의 관측수위 결과를 나타낸다. 모든 수치해석 결과는 2 - 3 m 구간에서 도수현상으로 인한 천이류를 보여주고 있지만 실험결과보다 수위가 과대산정 되었다. 이는 2차원 천수방정식이 수심방향으로 적분된 방정식으로 연직방향 유속변화에 대한 항은 무시되기 때문에 흐름이 정수압으로 고려되어 급변구간에서 소산되어야 할 에너지를 보존하였기 때문으로 판단된다.
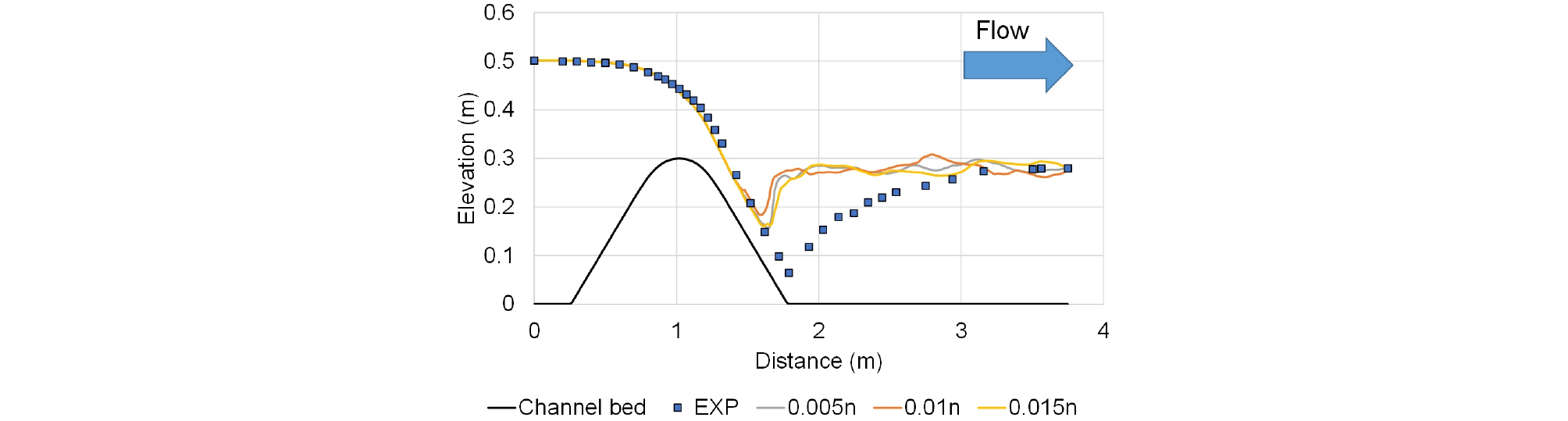
Fig. 4.
Simulation result of water level for sensitivity analysis (EXP: gauged water level of Hermann and Willi (1998), 0.005-0.015n: water level by Manning roughness coefficient).
모의결과의 정확성은 Table 2처럼 RMSE (root mean square error)와 결정계수 (R2)로 산정하였다. 모의결과, 각각 Manning 계수 (n)가 0.005, 0.01, 0.015일 때, RMSE는 0.062, 0.063, 0.059로 n = 0.015일 때 가장 적은 값을 나타냈고 결정계수는 0.857, 0.859, 0.873로 n = 0.015일 때 가장 큰 값을 나타냈다. 따라서 본 연구에서는 재현성이 제일 높은 n = 0.015의 값을 적용하여 예측모의를 수행하였다.
Table 1.
Parameters of computational model and simulation cases
Table 2.
Simulation reproducibility by Manning roughness coefficient
| Manning roughness (n) | RMSE (m) | R2 |
| 0.005 | 0.062 | 0.857 |
| 0.01 | 0.063 | 0.859 |
| 0.015 | 0.059 | 0.873 |
3.2 예측모의
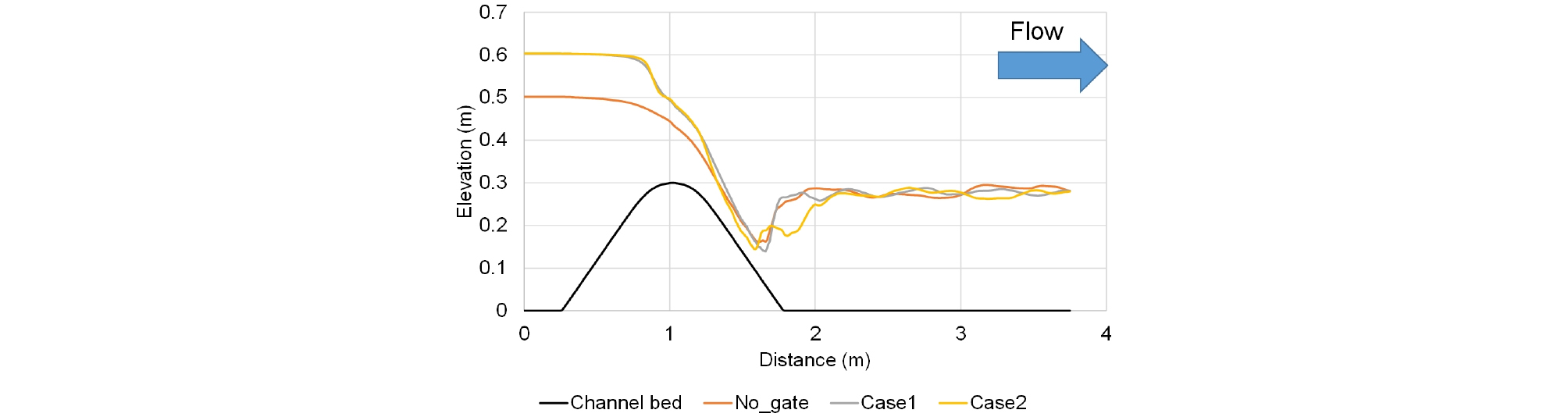
Fig. 5는 수문을 고려하는 Case 1 (Fig. 2 (b))과 Case 2 (Fig. 2 (c))의 계산된 수위를 나타낸다. 여기서 보여지는 수위는 Fig. 4와 동일한 앙상블 (ensemble)평균으로 산정되었다. 추가적으로, 수문을 고려하지 않은 “No_gate”의 모의결과 (=Fig. 4의n0.015) 도 같이 비교하였다. 모의결과를 비교해보면, No_gate, Case 1, Case 2의 순으로 각각 최대수위는 0.501 m, 0.602 m, 0.60 m로 상류가 발생하고 있는 지점인 위어 상류의 끝단 (toe of weir)부터 최상류부 (0 - 0.25 m 구간)까지 각각의 모의결과에서 수심이 일정하다. No_gate의 경우 위어 마루 (crest of weir)에 장애물이 없기 때문에 Case 1과 2보다 통수능이 더 커져서 상류부에서 배수효과로 인한 수위증가가 상대적으로 적게 나타난 것으로 판단된다.
최소수위는 모든 경우에 위어 하류부 끝단에서 발생하고 있으며 No_gate (0.160 m), Case 1 (0.139 m), Case 2 (0.144 m)로 Case 1에서 가장 낮은 수위가 계산되었다. 최소수심 발생지점 이후로는 에너지 소산으로 인하여 사류에서 상류로 변하는 천이류 흐름을 보여주고 있다.
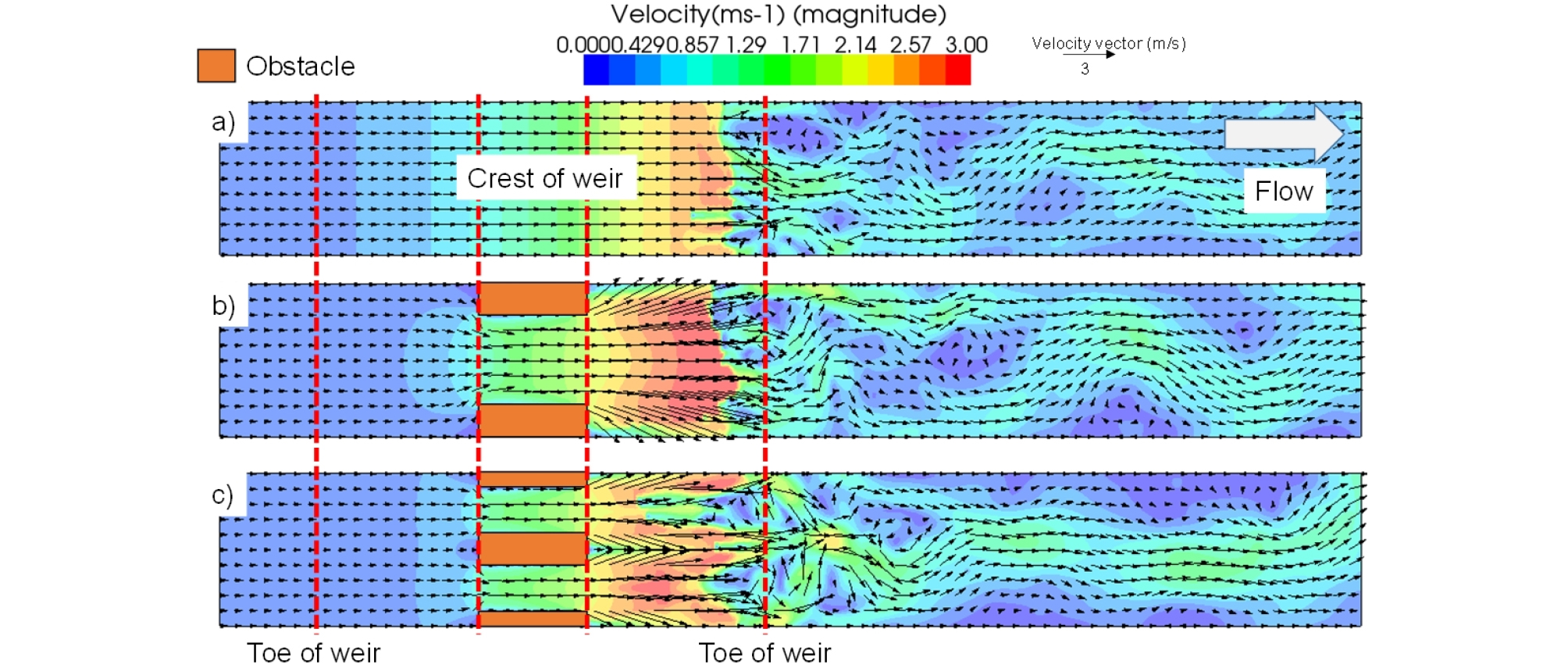
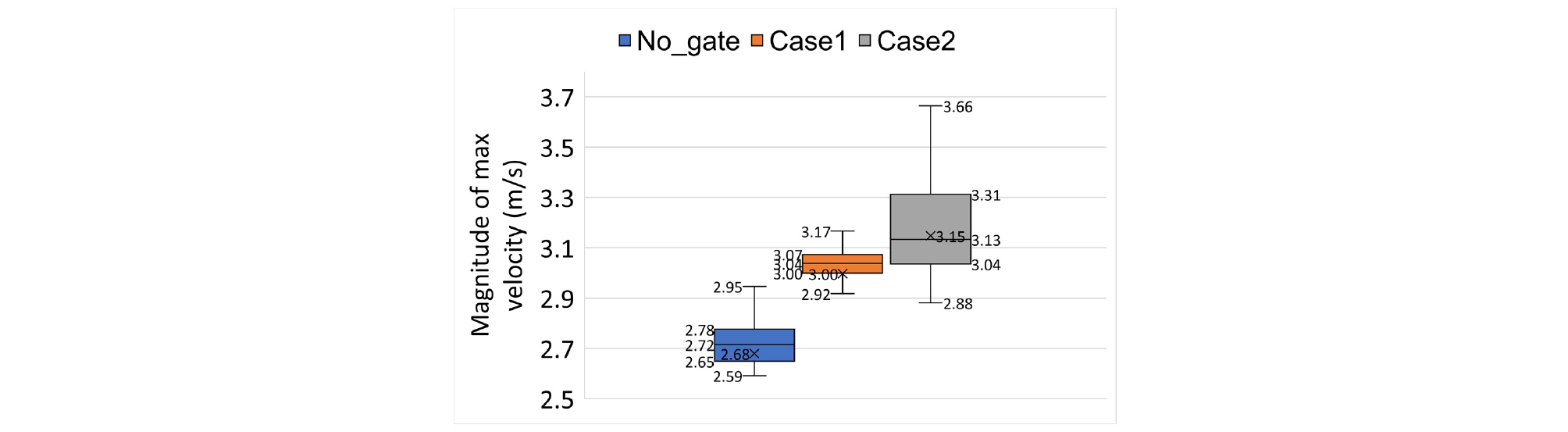
Fig. 6은 모의결과의 120 s시점에서의 유속분포를 나타내며, Fig. 7은 전체 모의시간 동안 나타난 최대유속의 범위를 보여준다. Fig. 6을 보면 모든 경우에서, 위어 상류단에서는 위어로 인해 하류단보다 낮은 유속 (<0.5 m/s)를 보여주며 위어 하류부에서는 급격하게 하도경사가 커지게 되어 상대적으로 높은 유속 (>2.7 m/s)을 보여준다. Fig. 7에서는 No_gate, Case 1, Case 2 순으로 최대유속이 각각 2.95 m/s, 3.17 m/s, 3.66 m/s으로 나타났으며, No_gate의 경우 단면축소의 영향을 받지 않았기 때문에 최대유속이 상대적으로 적었고 수로를 2개로 설정한 Case 2가 최대유속이 제일 높았다. Fig. 5에서 각각의 수위를 고려해볼 때에도, Case 1과 Case 2의 위어 마루에서의 총통수단면적은 매우 유사하지만 위어 하류부 끝단에서 Case 2의 최소수위가 더 낮게 나타났다. Case 1의 경우 물의 흐름이 위어의 정상부를 지나면서 양쪽 하안으로 하폭확대에 의한 하천 횡방향 유속이 발생 (Fig. 5 (b))하며 에너지소산 (energy dissipation)을 일으키게 되어 종방향 유속이 저감되는 효과가 발생했다. Case 2의 경우에도 동일하게 하폭확대로 인해 양쪽 하안으로 종방향 유속이 발생했다 (Fig. 6 (c)). 하지만 이와 동시에, 2개의 수로에서 하폭확대로 인해 개별적으로 발생한 횡방향 흐름이 하천중심선에 위치한 장애물의 하류단에서 충돌하면서 에너지 소산이 Case 1보다 적게 이루어지고, 오히려 횡방향 흐름의 이송각도가 충돌로 인하여 하천의 종방향으로 변하게 되었다. 결과적으로 Case 2에서 2개의 수로로 인해 위어 하류부에서 더 큰 유속을 초래한 것으로 판단된다. 따라서 같은 통수단면을 고려할 때는 수문의 갯수가 더 많은 위어가 방출유속이 더 클 것으로 판단되며, 이는 흐름의 영향을 지배적으로 받는 유사이송에도 영향을 끼쳐 실제 하천의 상황이었다면 하상변동을 야기할 수 있을 것으로 판단된다 (Williams and Wolman 1984, Jang and Woo 2009). 따라서 추후에는 이를 고려하는 실내실험과 수치해석을 세부적으로 수행하여 통수단면적과 수문의 갯수에 따른 유사이송과 하도변형을 모의 예측하는 연구가 필요할 것으로 판단된다.
3.3 모형의 한계 및 개선사항
일반적으로 불연속 흐름은 첨예한 지형적 특성 또는 정수압 가정이 적용되기 어려운 급변류나 충격파 (shock wave) 등으로 발생하게 된다. 불연속 흐름은 흐름모의에서 수치진동을 야기할 수 있으며 Nays2DH는 이러한 수치진동을 저감하기 위해 Direct force 기법과 유사한 흐름률 재산정 기법을 음해적으로 수행한다. 더 나아가 본 연구에서는 불연속 흐름이 발생할 수 있는 위어모형의 지형을 본 연구에서 고안된 4점평균법을 이용하여 재구성하였고, 그 결과로 위어 상류부가 정적으로 충분히 평형을 이루게 되는 120 s까지 실험값과 유사한 수위형태를 모의하였다. 한편, 흐름모형의 수치해석 검증에 널리 활용되는 Goutal and Maurel (1997) 및 그 결과를 상호 비교했던 수치해석 사례들을 보면, 대부분의 연구 (e.g., Kim and Han 2008, Kim et al. 2009)에서 모두 성공적으로 흐름모의를 수행했음을 보여주었으며, 이는 본 연구의 결과를 미루어 볼 때, Goutal and Maurel (1997)에서 제시한 하도지형의 곡선형태가 불연속 흐름의 수치진동 저감에 도움이 될 수 있었던 것으로 판단된다. 대신에, 첨예한 단차의 지형이었다면 수치진동의 발생정도가 달라졌을 것으로 추측된다. 따라서 추후 연구에서는 본 연구에서 활용한 4점평균법과 같은 하도지형의 전처리를 통해 불연속흐름의 수치진동을 저감하는 동시에, 위어의 고유형태 (e.g., 마루길이, 사면경사, 위어하부길이 등)를 반영할 수 있는 추가적인 수치모의 연구가 수행되어야 할 것으로 판단된다.
또한, 본 연구에서는 수문의 개방구성에 따른 상하류단 흐름변화에 대한 수치모형 개발연구의 초기단계로서 기존의 실내실험 자료를 토대로 (Hermann and Willi 1998) 보의 형상을 고려하여 흐름모의를 수행하였다. 하지만 본 연구에서는 보의 시간에 따른 가변적인 개방률을 고려하지는 않았다. 실무적으로는 가동보의 개폐를 고려하여 수위운영을 수행하는 경우가 많기 때문에 추가적으로 이를 고려해주는 것이 실제적인 예측모의를 위해 필요할 것으로 판단된다. 또한, 국가하천에 설치된 대부분의 보는 상한수위, 하한수위 등의 댐 관리 규정을 고려하여 운영되고 때문에 추후 연구에서는 세부적인 댐 관리 규정 (상한 수위, 하한 수위 및 홍수량, 갈수기 수량 등)과 홍수빈도에 따른 실제적인 중장기 모의예측 (Lee et al. 2015 참조)을 통한 연구가 필요할 것으로 판단된다. 더 나아가, 보의 운영은 상하류부의 하상변동에도 주요한 영향을 끼치므로 (Lee et al. 2014, Lee and Jang 2018) 이를 위해 유사이송을 추가적으로 고려하는 것이 필요할 것으로 판단된다. 이와 관련하여, Kang and Jang (2020)은 경우 2차원 흐름모형에 흐름률 통제함수 모듈을 시범적으로 적용하여, 가변적인 수문개방률에 따른 보 하류부의 흐름 및 지형응답을 모의하였으며, 이를 통해 수치해석과정에서 가변적인 수문개방률의 영향을 직접적으로 적용할 수 있는 가능성을 제시하였다. 따라서 본 연구에서 제시한 수치기법 및 개선사항과 더불어 Kang and Jang (2020)에서 시사한 수치모의 모듈개발의 적용 가능성에 기반하여 추후의 연구를 지속적으로 개선 및 발전 시킬 수 있을 것으로 기대된다.
4. 결론 및 제언
본 연구는 보의 영향을 고려한 자유월류 흐름해석을 실내실험 자료와 수치모형을 이용하여 수행 및 검증 후, 수문의 갯수에 따른 예측모의를 수행하였다. 우선은 위어마루에서 발생하는 한계류 수위를 보정하기 위해 본 연구에서 고안된 4점평균법으로 하도지형을 전처리 하였으며, 이를 통해 실내실험결과와 유사한 흐름을 모의할 수 있었다. 예측모의 결과에서는 수문의 갯수가 증가할 경우 보의 하류부에서 최대유속이 증가할 수 있음을 확인하였으며, 이는 동일한 통수단면적에서도 수문의 갯수에 따라 하류부의 흐름에 영향을 미칠 수 있다는 것을 보여주었으며 결과적으로 하상변동에도 영향을 줄 것으로 판단된다. 이러한 결과들은 추후에 보의 운영에 따른 흐름 및 유사이송 등을 고려하는 수리학적 연구의 기초자료가 될 것으로 기대된다.