1. 서 론
2. 연구방법
2.1 연구지역
2.2 자료 수집
2.3 연구방법
3. 결과 및 고찰
3.1 강우 및 유량자료 수집 결과
3.2 입력자료 및 타겟자료 생성결과
3.3 CNN 구조
3.4 모형 훈련 및 결과
3.5 산정 결과 및 모형 평가
4. 결 론
1. 서 론
강우에 의한 유출량은 지표면상의 수자원으로 인간활동이나 자연계 동식물에게 매우 중요한 필수 요소이나, 유출량의 급작스런 증가는 물리적 환경 파괴 및 인간활동에 직접적인 피해 발생을 야기한다. 이에, 강우에 따른 유출량 산정의 중요성이 매우 높은데, 이를 해결할 수 있는 방안이 유출모형 (discharge model)의 개발과 그 활용이다. 유출모형은 수자원 관리, 계획, 수문학적 설계 등에 중요한 역할 수행이 가능한 과학적 기법인 동시에 (Othman and Naseri 2011), 수자원을 활용하는 분야의 정책 수립에도 도움을 줄 수 있다 (Singh et al. 2013).
강우-유출 관계는 강우 패턴 및 유역의 물리적 요소뿐만 아니라, 다양한 공간적 및 시간적 변화에 기인하는 복잡한 수문학적 현상으로 (Maier et al. 2010), 유출모의는 매우 까다로울 수밖에 없는 특징을 갖고 있다.
이러한 복잡성이 존재함에도, 과거부터 현재까지 강우-유출량 관계를 규명하기 위한 노력이 전개되고 있는데, 전통적으로는 강우와 유출량간의 경험을 토대로 유출량을 모의하는 방법론을 채택했으며, 근래에는 전통적 방법론을 확장하여 개념적 모형 (conceptual model) 또는 경험적 모형 (empirical model) 을 개발해오고 있다. 개념적 모형은 물리적 법칙에 기반하여 수문학적 순환을 표현한 모형 (Nourani et al. 2012)을 일컬으며, 경험적 모형은 개념적 모형의 대안으로 물리적 법칙을 활용하지 않고, 입력 데이터와 결과 데이터간의 안정적 관계를 이용하여 개발된 모형이라는 특징을 갖는다 (Patel and Joshi 2017).
경험적 모형은 복잡한 자연현상을 수식으로 표현해야 하는 개념적 모형에 비해 모형 구축이 상대적으로 단조로워, 많은 선행연구에서 경험적 모형을 사용하는 빈도가 높게 나타나고 있다. 특히, 경험적 모형에 포함되는 인공신경망 (artificial neural network, ANN) 이론은 과거 학계에서 외면 받았으나, 최근에는 4차 산업혁명을 대표하는 고유명사로 부각되면서, 여러 분야에서 ANN을 사용하는 추세가 강하게 나타나고 있다. 또한, 최근 GPU (graphic process unit) 및 하드웨어의 획기적 기술 발전과 빅데이터 등으로 이론 수준에서 머무르고 있던 ANN 관련 다양한 이론이 구현되면서 높은 성능이 보고되고 있다. 이와 함께, 신경망의 층 (layer)이 더욱 깊어진 딥러닝 (deep learning)이나, 다양한 구조의 ANN 등이 개발되면서, ANN은 활용분야의 확대와 급진적인 정확도 상승 등의 결과를 보이고 있다.
그러나 일부 개념적 모형을 선호하는 연구자들은 유출모형 연구에 ANN을 이용하는 것에 대해 ANN은 black-box 모형의 일종으로, 입력 데이터와 결과 데이터간의 역학관계를 명확히 설명할 수 없기에 강우-유출량 모의에 ANN을 활용하는 것은 적합하지 않다는 비판은 보고된 바 있다 (Kalteh 2008). 그럼에도 잡음 (noise)이 있거나 불충분한 경우에도 불구하고, 여러 학습 법칙을 통해 입력 데이터와 결과 데이터간의 비선형적 구조를 표현할 수 있는 ANN의 이점을 이용하여, 많은 연구자들은 ANN을 통해 복잡한 유출모형을 개발하고 있다. 이와 관련하여 모형의 산정 성능 및 효율성 등에 대해 ANN 모형이 개념적 모형에 비해 더 우수한 것으로 보고하고 있다 (Zhang and Govindaraju 2000, Farias et al. 2013, Shoaib et al. 2016, Mishra and Karmakar 2019).
앞서, 유출모형에 ANN을 활용한 선행연구는 ANN 내의 은닉층 (hidden layer) 및 해당 은닉층 내의 가중치가 연결되는 노드 (node) 개수를 조절하여 높은 성능을 나타낼 수 있는 최적의 ANN 구조 (architecture)를 찾아내는 주제이거나, 해결하고자 하는 문제의 유형에 따라 ANN의 학습방법 또는 연구자가 제안하는 특정 학습방법을 통해 높은 성능을 보고하는 주제 등인 경우가 주를 이루고 있다. 이와 같은 연구의 특징은 일차원적 벡터 (N × 1 또는 1 × N)로 이루어진 입력 및 결과 데이터간의 관계를 최적화하거나, 회귀모형 (regression model)의 구조를 이용하여 ANN으로 회귀계수를 추정하는 등의 방법론을 이용하고 있어 (Wu and Chau 2011, Kasiviswanathan and Sudheer 2013, Maca 2014, Benzineb and Remaoun 2016), 현재 다른 목적을 위한 다양한 딥러닝 알고리즘을 유출모의에 활용되고 있지 못한 상황이다. 이에, 본 연구에서는 유출모형 개발을 위해 다양한 알고리즘을 적용 연구를 수행하고자 1차원 벡터를 입력자료로 사용하는 기존의 방법론에서 벗어나, 2차원 행렬 구조의 이미지를 입력자료로 하는 딥러닝 기반의 유출모형을 개발하고 그 성능을 제시함으로, 유출모형 개발의 다변화 도모 및 활용 가능성을 제시하고자 한다.
2. 연구방법
2.1 연구지역
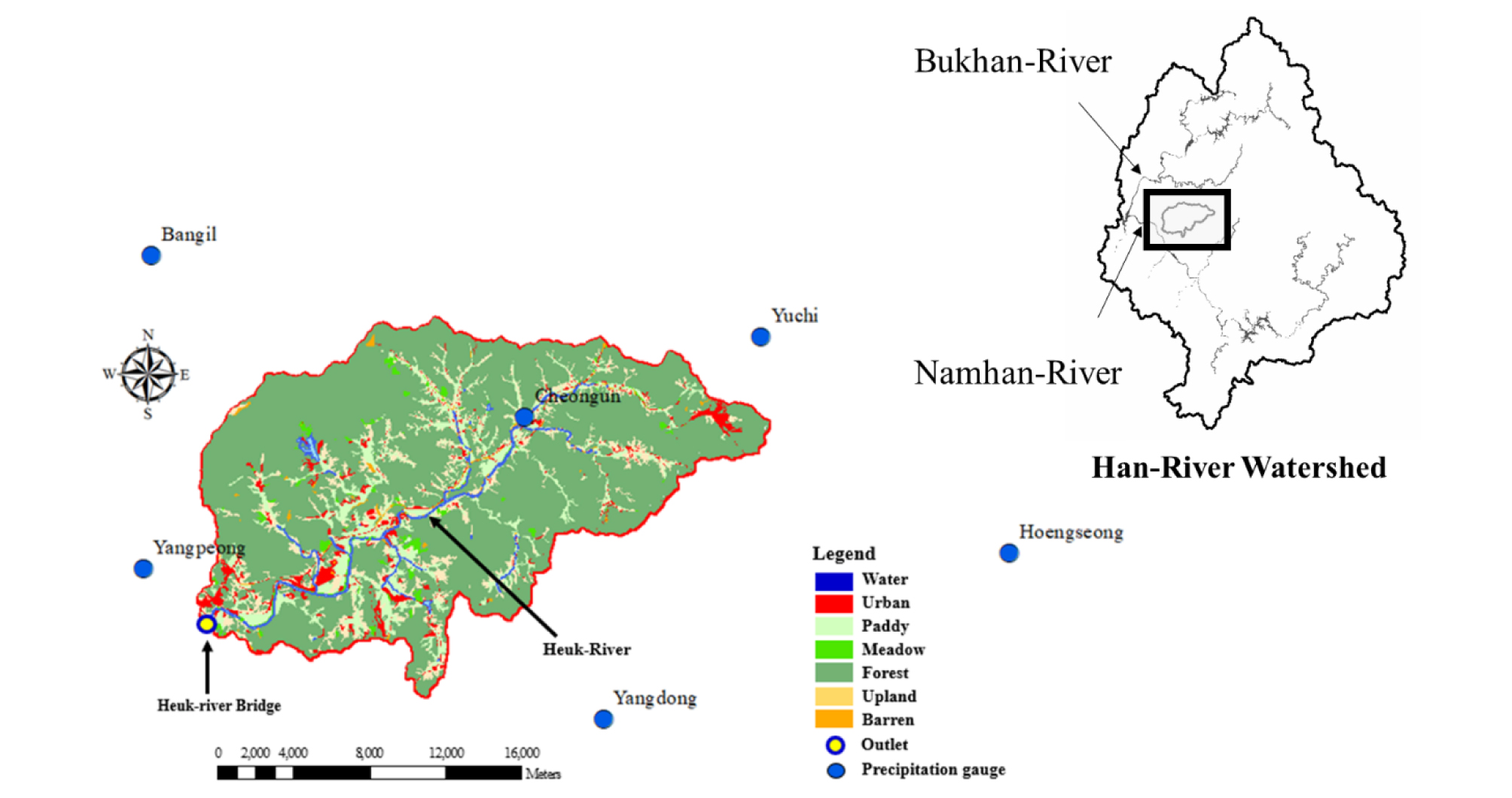
연구지역은 환경부가 수질오염총량관리제도 시행을 위해 설정한 단위 유역 중 행정구역상 경기도 양평군에 속해 있으며, 권역상으로는 한강권역에 포함되는 흑천A 단위유역 (E 127° 31' 55.39", N 37° 27' 37.69")이다 (Fig. 1). 흑천 A 유역은 수질오염총량관리제도에 의해 설정된 목표수질를 준수해야 하는 지역으로, 1년 중 목표수질을 초과한 일수를 산정하여 목표수질 위반여부를 평가하며, 위반시 강력한 패널티가 부여된다. 이에, 목표수질 준수에 대해 매우 예민한 지역인데, 수질변화가 유량변화에 의존적으로 나타나기에, 일유출량 산정 또는 검토 등이 반드시 요구되는 지역이다. 흑천 A유역은 타 행정구역 (시 ‧ 군단위 이상)으로부터 유입되는 하천이 없고, 양평군 청운면 신론리 성지봉에서 발원하는 흑천이 주하천인 유역이다. 흑천 A유역은 토지이용의 변화가 거의 없으며, 특별대책지역 및 자연보전권역 등으로 규제가 강한 지역이다. 흑천 A 유역의 면적은 314.0 km2, 하천장은 42.9 km, 평균 경사는 27°이며, 산림이 79%, 농림지역이 15.2%로 전형적인 농촌지역이다 (Table 1).
Table 1.
Summary of study area
| Land cover | Water | Urban | Barren | Pasture | Forest | Paddy | Upland | Total |
| Area (km2) | 8.32 | 10.87 | 7.10 | 1.36 | 238.39 | 25.99 | 21.99 | 314.03 |
| Percentage (%) | 2.7 | 3.5 | 2.3 | 0.4 | 75.9 | 8.3 | 7.0 | 100.0 |
2.2 자료 수집
본 연구에서 활용하고자 하는 자료는 강우, 유량, 토지이용도 및 토양도 등 4개 항목이다. 자료의 수집기간은 2006년 1월 1일부터 2019년 12월 31일까지이다. 본 연구에 필요한 자료는 모두 온라인상에서 제공하는 자료를 활용하였는데, 강우자료는 기상청 (KMA 2020), 유량 및 토양도는 국가수자원관리종합정보시스템 (WAMIS 2003), 토지이용도는 환경공간정보서비스 (EGIS 2010)에서 수집하였다. 유량자료는 Fig. 1의 흑천교에서 측정한 일단위자료이며, 강우 자료는 연구지역 내외에 위치하고 있는 강우측정소 6개소 (방일, 유치, 청운, 양평, 양동, 횡성)의 일단위 자료이다. 여기서 강우, 유량자료는 앞서 언급한 바와 같이 일단위 자료이나, 해당 자료를 제공하는 기관에서는 일누적 자료로 제공함에 따라, 일유량 측정 시점 및 종점 등을 고려하지 않고, 1일 동안의 발생량으로 단순화하여 모형에 적용하였다.
토지이용도 및 토양도의 1개 grid가 30 m × 30 m을 나타내는 형식으로 작성되어 있으며, 축적은 1:5,000의 자료이다. 토지이용도는 대분류 시스템으로 수역, 도심, 나지, 초지, 산임, 논 및 밭 등, 7개 항목으로 되어 있으며, 토양도는 59개의 물리적 특성을 갖는 자료이다.
2.3 연구방법
본 연구는 딥러닝 중 하나인 합성곱 신경망 (convolution neural network, CNN)을 활용하여 유출모형을 개발하고자 하였다. CNN은 지도학습 (supervised learning) 방법을 이용하는데, 지도학습은 문제와 답 (target)을 하나의 자료셋 (data set)으로 신경망에 주입하고 훈련시킨 후, 신경망이 경험하지 못한 새로운 문제에 대한 적절한 답을 찾아내는 방법으로 정의할 수 있다.
이러한 기본 개념을 바탕으로 연구 과정은 다음과 같은 절차를 갖는다. 1) 2차원 [N × M] 행렬구조의 이미지 자료 (image data)와 [1 × K]차원의 타겟 자료 (target data)를 생성하여, 입력 데이터셋 (input data set)과 테스트 데이터셋 (test data set)으로 구분한다. 여기서 입력 데이터셋은 모형의 학습 및 검정을 위한 자료이며, 테스트 데이터 셋은 모형의 산정성능을 평가하기 위한 자료이다. 여기서, 입력 데이터셋은 학습 데이터셋 (training data set)과 검정 데이터셋 (validation data set)로 구분한다. 그 다음순서로, 2) CNN 모형을 연속변수 모의가 가능한 모형의 구조로 변경한다. 3) CNN 모형에 image의 속성과 유출량간의 비선형적 관계를 학습시킨 후, 유출을 산정하는 순으로 진행하고, 4) 마지막으로 모형 평가를 시행하여 모형의 적합성 및 정확성을 나타내는 순서로 진행하였다.
2.3.1 입력 자료셋
CNN은 RGB (red, green, blue) scale 또는 gray scale 등의 이미지를 입력자료로 받아 2차원 공간상의 색값 (color value) 및 위치 등의 특성을 추출하여 문제를 해결하는 알고리즘을 이용한다. 본 연구에서도 CNN이 인식을 할 수 있도록 입력자료로 이미지를 이용해야 하는데, 연구의 특성상 일반 사진자료가 아닌 유역조건 및 강우 등의 영향이 반영된 수치적 (numerical) 이미지를 사용해야 하는 난해점이 있다. 이를 해결하기 위해 유출이 강우 발생시 토지이용 및 토양특성, 선행강우 등의 영향으로 각기 다르게 나타나는 현상을 착안하여 이미지 생성에 활용하고자 하였는데, 이에 부합하는 방법으로 자연자원보호청 (National Resource Conservation Service, NRCS)의 전신인 토양보존국 (Soil Conservation Service, SCS)에서 발표한 수문학적 토양피복형수 (curve number, CN)가 적합하다고 판단하였다. 이를 더욱 가능하게 하는 CN의 특징으로 본 연구에서 고려하고자 했던 토양의 물리적 특성, 토지이용, 및 선행토양습윤조건 (antecedent soil moisture condition, AMC) 등을 1 - 100 사이의 정수로 나타낼 수 있으며, 이를 통해 상이한 유출량 추정이 가능하다는 장점을 갖고 있다 (Rallison 1980).
특히, 여러 선행연구와 같이 유역 전체를 대표하는 CN을 산정하는 방법이나, 면적가중평균 (area weighted mean)을 이용한 CN 할당 방법이 아닌, 사진의 픽셀과 같이 기존보다 더 작은 단위로 CN을 할당할 경우 이미지로 나타내기에 적합할 것으로 판단하였다.
이에, 본 연구에서는 토지이용 및 토양도 등을 모두 30 m × 30 m의 grid 단위로 통일하고, 각 grid에 CN을 할당하고자 하였다. CN 할당 방법은 NRCS에서 제안한 Eqs. 1 and 2를 그대로 이용하였다.
| $$Q=\frac{(P-0.2S)^2}{\;P+0.8S}\;(P>Ia)$$ | (1a) |
| $$Q=0\;\;\;\;\;\;\;\;\;\;(P\leq Ia)$$ | (1b) |
| $$S=\frac{25400}{CN}-254$$ | (2) |
여기서 Q는 유출량, P는 강우, S는 잠재저류수량을 의미한다. 이에 더하여, NRCS에서 제안한 바와 같이 유효우량, 5일 누적강우, 비수기 (dormant) 및 성수기 (growing season) 등에 따른 선행토양습윤조건 변화, 선행토양습윤조건에 따른 CN의 조정 등을 grid 마다 준용하였다. 다만, NRCS에서 제공하는 CN은 국내에서 사용하기 적합하지 않아, 국토해양부 설계홍수량 산정요령 (MLTM 2012)에서 제시한 CN을 사용하였다.
유출 산정에 필요한 유역 내 강우량 산정도 grid 단위로 일치시켜야 하기 때문에, 티센 폴리곤 (Thiessen polygon) 방법을 사용하지 않고, 역거리가중법 (inverse distance weighted, IDW)를 사용하였다. 티센 폴리곤을 사용할 경우 폴리곤 경계에서 수치 변화의 불연속성이 나타나 실제 강우와 왜곡 또는 차이를 발생시키는데, 역거리 가중법은 토블러 법칙 (Tobler’s law)을 기반으로한 내삽방법이기에 이를 사용할 경우, 티센 폴리곤의 불연속성을 보완할 수 있다. 역거리 가중법 계산은 토지이용 및 토양도와 같은 해상도로 동일하게 설정한 후, ArcGIS 10.0을 이용하여 계산하였다. 최종적으로 grid 마다 유출값이 담긴 2차원 배열의 자료는 이미지 파일 형식 중 하나인 TIF 파일로 변환하여 입력자료로 활용하였다.
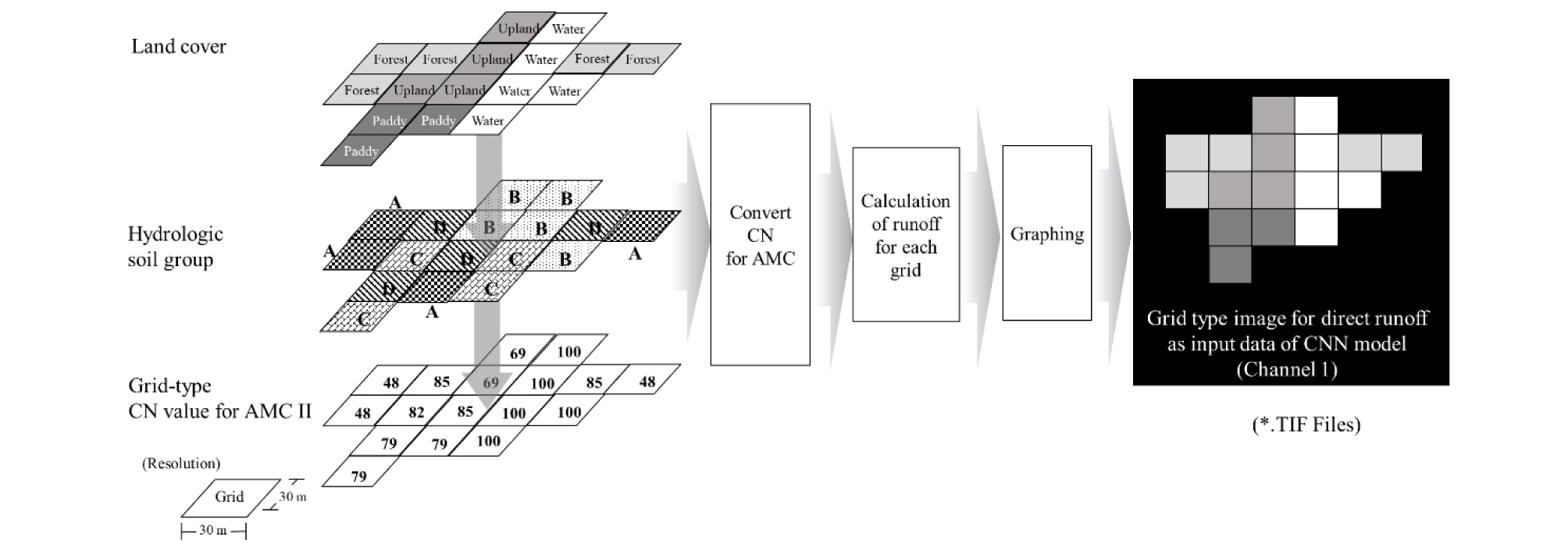
지금까지의 각 grid별 유효우량, 5일 누적강우 판단, 비수기 및 성수기 조건반영, 선행토양습윤조건 적용, 선행토양습윤조건에 의한 CN의 조정, 잠재저류계산 및 유출 산정 등의 절차는 모두 오픈소스 언어인 Python 3.7 (2018)을 이용하여 시행하였으며, 이와 관련한 개략적 이미지 생성 과정은 Fig. 2와 같다.
2.3.2 타겟 자료
앞서 언급한 바와 같이 본 연구에서는 입력자료와 타겟 자료를 하나의 자료셋으로 구성해야 되야 하는데, 타겟 자료는 복잡한 이미지 생성 방법과는 달리, 간단하게 생성된 이미지의 따른 해당 일자의 유출량을 바로 타겟 자료로 사용가능하다.
2.3.3 CNN 구조 설정
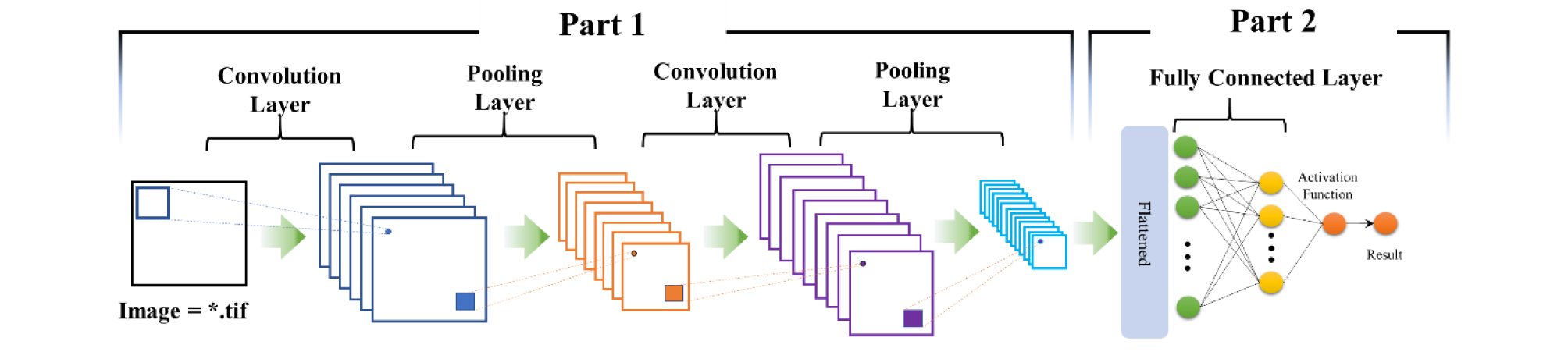
CNN은 딥러닝의 구조 중 하나로, 뇌의 시각 피질이 물체를 인식할 때 동작하는 방식에서 영감을 얻은 모델이다. 관찰 대상을 이미지로 인식하여 분류하는 문제에 특화된 신경망으로 Fig. 3과 같은 구조를 갖는다. CNN은 Fig. 3과 같이 2개의 part로 구분할 수 있는데, part 1은 CNN의 핵심 기능인 이미지 특성을 추출하는 층으로, 합성곱 층과 풀링 층의 반복으로 구성되어 있다. part 2는 완전 연결층 (fully connected layer)으로 part 1에서 출력된 이미지 특성을 입력층으로 인식하며, 출력층 사이에 여러 개의 은닉층으로 구성된 심층 신경망 (deep neural network, DNN)이다. 여기서 완전 연결층의 입력 값은 합성곱 층과 풀링 층을 통과한 값으로, 합성곱 층의 커널에 의해 압축된 이미지와 이를 다시 풀링층에 의해 추출된 값과 특성값으로 이루어진 값을 의미한다.
본 연구에서는 모의하고자 하는 유출이 불특정 연속변수이기 때문에, 분류 문제와 같은 이산 변수 산정을 위한 CNN 구조를 그대로 사용하기에는 부적합하다. 이에, CNN의 구조를 변경해야 하는데, CNN의 핵심기능인 이미지 특성 추출을 위한, Fig. 3의 part 1은 그대로 사용하되, part 2의 구조를 선형회귀층 (linear regression layer) 구조로 변경하여 모형에 반영하였다. 일반적으로 CNN 모형에서 사용하는 binary crossentropy layer이나 softmax layer를 사용하지 않고, 선형회귀층으로 변경한 이유는 binary crossentropy나 softmax 함수는 이산변수 산정을 위한 함수층이기에 연속변수 산정에는 적합하지 않기 때문이다.
CNN의 모형 설계, 구현 및 운용 등을 위한 환경은 모두 Google에서 공개한 머신러닝 라이브러리 (machine learning library)인 Tensorflow (2019)를 backend로 하는 Keras를 이용하였으며, Python에서 구현하고 실험을 시행하였다. Keras는 Python으로 작성된 고수준 딥러닝 API (application programming interface)로, Tensorflow의 특수 기능을 모두 지원하며, 딥러닝 모형 구현의 유연성이 매우 높다. 또한, CPU와 GPU를 효율적으로 사용할 수 있기에 빠른 실험이 가능하다는 특징을 갖는다 (Keras 2019).
2.3.4 모형 평가
모형의 평가를 위해서 관측값과 모형을 통한 산정값을 비교하여 모형의 성능을 판단하였다. 이를 위해 Pearson 상관계수 (Pearson correlation coefficient, r), NSE (Nash-Sutcliffe efficiency) 및 RMSE (root mean square error) 등의 3가지 방법을 사용했다.
r는 Eq. 3을 통해 -1부터 1까지의 범위로 표현되며, 관측값과 산정값간의 선형성을 나타낸다. r가 1에 가까울수록 모형의 산정값과 관측값의 선형성이 강해지는 것을 의미하며, 1로 수렴할수록 모형의 성능이 우수한 것으로 판단한다.
| $$r=\frac{\sum_{i=1}^n(y_i-\overline y)\;(y'_i-\overline y')}{\sqrt{\sum_{i=1}^n}{(y_i-\overline y)}^2\;\sum_{i=1}^n\;{(y'_i-\overline y')}^2}$$ | (3) |
NSE는 Eq. 4와 같이 나타내는데, 결과값이 1일 경우 모형의 결과와 관측값이 완벽하게 정확하다는 것을 의미한다. 또한, 0으로 수렴할수록 모형의 성능이 좋지 않다는 것으로 판단한다.
| $$NSE=1-\frac{\sum_{i=1}^n{(y_i-y'_i)}^2}{\sum_{i=1}^n(y_i-{\overline y)}^2}$$ | (4) |
RMSE는 Eq. 5를 통해 모형이 얼마나 관측값에 가깝게 산정하는지를 보여주며, 그 범위는 해당 데이터의 범위 내에서 0부터 무한대로 나타낸다. RMSE 자체에 대한 평가기준은 명확하지 않으나, 0으로 가까울수록 모형의 결과가 관측값에 일치함을 의미한다.
| $$RMSE=\sqrt{\frac{\sum_{i=1}^n{(y_i-y'_i)}^2}n}$$ | (5) |
여기서 yi, y΄i는 관측값과 산정값을, , 는 관측값 및 산정값의 평균을 의미한다.
3. 결과 및 고찰
3.1 강우 및 유량자료 수집 결과
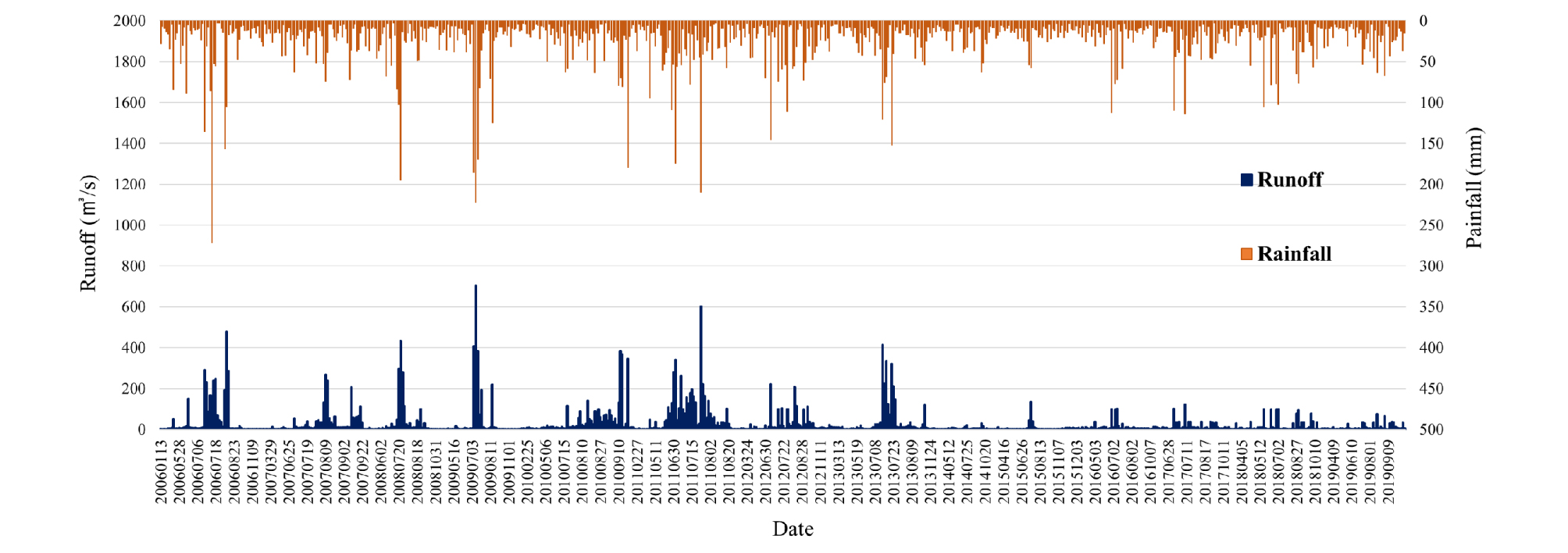
자료수집기간인 2006년 1월 1일부터 2019년 12월 31일까지의 강우 발생 횟수는 전체 680회로 나타났다. 동일기간의 강우량의 범위는 Fig. 4와 같이 2.2 - 271.6 mm로 나타났으며, 유출량의 범위는 0.18 - 704.3 m3/s으로 나타났다. 강우 발생 횟수는 2010년에 67회로 가장 높았으며, 2014년에 29회 가장 낮은 횟수를 보였다. 평균 강우량은 2009년에 35.1 mm 로 가장 높게 나타났으며, 2015년에 19.5 mm로 가장 낮게 나타났다. 평균 유출은 2011년에 75.4 mm로 가장 높았으며, 2014년에 5.4 mm 가장 낮은 값을 보였다 (Table 2).
Table 2.
Annual number of recording, runoff and rainfall
3.2 입력자료 및 타겟자료 생성결과
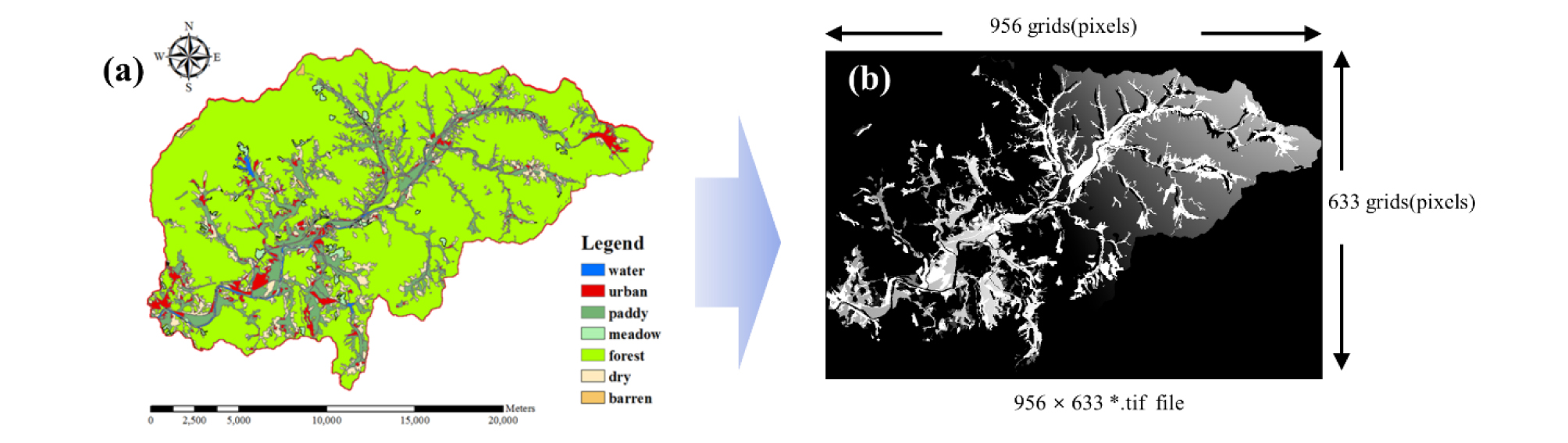
앞서 언급한 바와 같이 자료 수집 기간 중 활용 가능한 일단위 유효 강우는 전체 680회로 나타나, 680개의 이미지를 생성했다. 생성된 이미지의 예시는 Fig. 5와 같다. 여기서, Fig. 5 (a)는 이미지 생성 이전의 grid 형식의 토지이용 상태를 나타내며, Fig. 5 (b)는 본 연구의 이미지 생성 방법론을 통해 생성된 이미지를 보여준다. 생성된 이미지는 grid 단위로 횡축 및 종축이 각각 956개 및 633개 grid의 크기를 갖으며 (956 × 633), TIF 형식의 파일이다 (Fig. 5 (b)). 또한, 생성된 이미지는 gray scale로, 흰색으로 표현될수록 유출량이 높은 것을 의미하며, 검은색으로 나타낼수록 유출량이 0으로 수렴하는 것을 의미한다.
생성된 680개의 이미지와 이에 대응하는 유량 관측값은 하나의 자료 셋으로 함께 CNN 모형에 입력되나, 앞서 언급한 바와 같이 입력 자료셋과 테스트 자료셋으로 구분하고자 약 70%에 해당되는 501개의 자료는 CNN 모형을 훈련하기 위한 입력 자료셋으로, 나머지 179개의 자료는 모형의 산정값을 평가하기 위한 테스트 자료셋으로 설정하였다. 또한, 입력 데이터셋 중 80%에 해당되는 400개의 자료는 훈련 자료셋으로, 나머지 101개의 모형 검정을 위한 검정 자료셋으로 구분하였다. 자료의 구분 기준은 명확하기 않고, 주로 연구자가 임의로 설정하는데, 많은 선행연구에서는 입력과 테스트의 비율을 7:3이나 8:2 수준으로 구분하여 사용하여 실험을 진행하는 추세이다.
3.3 CNN 구조
본 연구에서 설계한 모형의 구조는 크게 두 가지 방향성을 갖는다. 첫 번째 방향은 CNN의 이미지 특성 추출 기능을 활용하기 위해 합성곱 층 (convolution layer)과 풀링 층 (pooling layer)의 반복으로 구성하고자 하였으며, 두 번째 방향은 연속 변수 모의가 가능하도록 완전 연결층에 대한 구조를 변경하고자 하였다. 이에 따라 본 연구에서 설계한 CNN의 구조는 합성곱 층과 최대풀링 층가 교차하면서 5회 반복되는 구조를 갖으며, 이는 Fig. 3의 part 1에 해당된다. 또한, 완전 연결층은 덴스 층 (dense layer)로 구현되며, 3개 층으로 연결되어 있는데, 두 번째 덴스 층 다음에 과적합 (overfitting)을 피하기 위해 배치 정규화층 (batch normalization layer)이 추가되는 구조로 설계하였다. 마지막 덴스 층은 선형회귀층으로 설정하여 연속변수가 출력할 수 있도록 하였다 (Table 3).
Table 3.
Summary of convolution neural network
합성곱 층 연산은 이미지 필터의 일종인 커널 (kernel)이라고 불리는 별도의 2차원 평면 함수를 이용하는데, keras에서는 커널의 크기를 설정할 수 있도록 하고 있다. 본 모형의 첫 번째 합성곱 층의 커널은 5 × 5의 크기로, 나머지 합성곱 층의 커널은 2 × 2 크기로 설정하였다. 또한 커널의 개수도 정할 수 있는데, 5개의 합성곱 층의 커널 수는 차례대로 32, 64, 128, 256 및 512개로 설정하였다. 또한, 모든 합성곱 층의 활성화 함수는 정규화 선형 함수 (rectified linear unit, ReLu) 함수로 설정하였는데, ReLu 함수는 일반적으로 CNN 모형에 많이 사용되며, 기울기 값이 사라지는 현상 (gradient vanishing)을 피할 수 있으며, 모형의 최적화 효율이 높은 것으로 보고되고 있다 (Ide and Kurita 2017, Chen and Ho 2019).
풀링 층은 이미지의 크기를 줄이면서 중요한 정보만 남기는 방식의 하위 샘플링 (sub-sampling) 기법이며, 이러한 특징으로 컴퓨터 메모리를 효율적으로 사용 가능하고, 계산한 정보가 줄어들기 때문에 과적합을 방지하는 효과가 있다. 풀링은 최대 (max pooling)과 평균 풀링 (average pooling)방법이 있는데, 평균 풀링은 정보의 손실을 발생시킬 수 있기 때문에, 본 모형에서는 최대 풀링 사용하였다. 풀링도 커널과 마찬가지로 크기를 설정할 수 있는데, 본 연구에서는 2 × 2 크기로 설정하였으며, 풀링의 크기를 2 × 2로 설정했기 때문에 이미지가 층을 거칠 때마다 크기가 반감되는 특징을 갖게 된다.
완전 연결층은 2차원 데이터 구조의 합성곱 층의 결과를 입력 데이터로 받아 1차원으로 변형시켜 (flatten) 덴스 층으로 전해주는 DNN 구조이나, 2차원 데이터 구조를 1차원으로 변형시키는 특성을 갖고 있어, 이미지의 공간적 특성을 무너뜨리는 특징을 갖는다. 합성곱 및 풀링 층을 거치면서 이미지의 정보를 유지하고 있기 때문에 안정적인 모형 학습이 가능하다.
Table 2에서 나타난 바와 같이, 본 모형의 신경망 가중치의 개수를 의미하는 총 매개변수 (total params)는 5,272,321개로 나타났으며, 훈련되는 가중치의 개수 훈련 매개변수 (trainable Params)는 5,272,065, 훈련되지 않는 가중치의 갯수 (non-trainable params)는 256개로 나타났다. 여기서 훈련되지 않는 가중치의 갯수가 발생한 이유는 배치정규화층에 의한 것으로 해당 층의 노드 (node) 갯수가 128개이기 때문이다. 최종적으로 마지막 덴스 층의 활성화 함수는 선형으로 설정하여, 연속변수를 도출할 수 있도록 하였으며, 노드 개수를 1개로 설정하여, 타겟 자료와 매칭될 수 있도록 하였다.
3.4 모형 훈련 및 결과
모형을 훈련시키는 것은 최적화 (optimizer) 알고리즘을 이용하여 반복 계산 및 업데이트를 통해 신경망 가중치 (parameter)를 최적화하는 것으로 설명할 수 있다. 즉, 신경망 가중치의 최적화는 관측값과 산정값간의 오차를 최소로 줄여가는 행위로 설명할 수 있다. 신경망 분야에서는 오차를 줄이는 방법으로 확률적 경사 하강법 (stochastic gradient descent, SGD)을 가장 기본적인 알고리즘으로 사용한다. SGD는 가중치를 업데이트 할 때 마다 미분을 통해 기울기를 구한 다음 기울기가 낮은 쪽으로 업데이트 하면서 손실를 줄이는 과정을 거친다. loss는 오차와 비슷한 개념이며, DNN은 대게 loss를 줄이는 방향으로 훈련한다. 여기서 확률적이라는 의미는 가중치 전체를 한 번에 계산하는 것이 아닌, 확률적으로 일부 샘플을 구해서 조금씩 나눠서 계산한다는 의미이며, 학습 횟수가 충분하면, SGD는 효과가 있으나, 잡음이 심하며, 속도가 매우 느리다는 단점이 있다.
최근에 들어와 SGD의 단점을 개선하고자 SGD를 바탕으로 학습 속도 및 정확성을 상승시키기 위해 개발된 Momentum, Nesterov Accelerated Gradient (NAG), Adagrad, Nadam, AdaDelta, RMSProp 및 Adam 등의 최적화 알고리즘이 이용되고 있는데, RMSProp는 Adagrad 보다 좋은 학습결과를 나타내며, Adagrad의 단점을 보완한 Adadelta 보다도 더 나은 학습 결과를 나타내고 있다. 또한, RMSProp는 Momentum을 적용할 수 있어, Momentum 상수를 적용함으로써 이전 기울기에 대한 이동 벡터를 적용할 수 있기 때문에 현재 Adam과 함께 많이 사용되고 있다 (Lim et al. 2017). 이와 함께, 모형의 학습 결과 및 일반화 등을 판단하기 위한 방법으로는 CNN 모형 평가는 일반적으로 정확도 (accuracy)를 측정항목 (metric)으로 이용하는데, 연속변수 산정에 대한 측정항목으로 평균절대오차 (mean absolute error, MAE)를 사용한다.
본 연구에서는 손실함수를 Eq. 6과 같이 평균제곱오차 (mean square error, MSE)를, 가중치 최적화 알고리즘은 RMSProp을, 학습률 (learning rate)은 0.0001로, 학습횟수 (epoch)는 500회로 설정하였다. 또한, 모형의 측정항목으로 Eq. 7에 의한 평균절대오차 (mean absolute error, MAE)를 이용한다.
| $$NSE=\frac1n{\textstyle\sum_{i=1}^n}{(y'_i-y_i)}^2$$ | (6) |
| $$MAE=\frac1n{\textstyle\sum_{i=1}^n}\left|y'_i-y_i\right|^2$$ | (7) |
여기서 yi 및 y΄i는 관측값과 산정값을 의미한다. 또한, MSE 및 MAE는 0으로 수렴할수록 모형의 성능이 높은 것을 의미한다.
모형은 loss, validation loss, MAE 및 validation MAE 등의 결과를 이용하여 학습 결과를 평가는데, 여기서 loss 및 MAE는 입력 자료셋 중 훈련 자료셋에 대한 것으로 각각 모형의 학습 결과 및 산정 성능을, validation loss 및 validation MAE는 검정 자료셋에 대한 것으로 각각 모형의 일반화를 위한 학습 결과 및 산정 성능을 나타낸다.
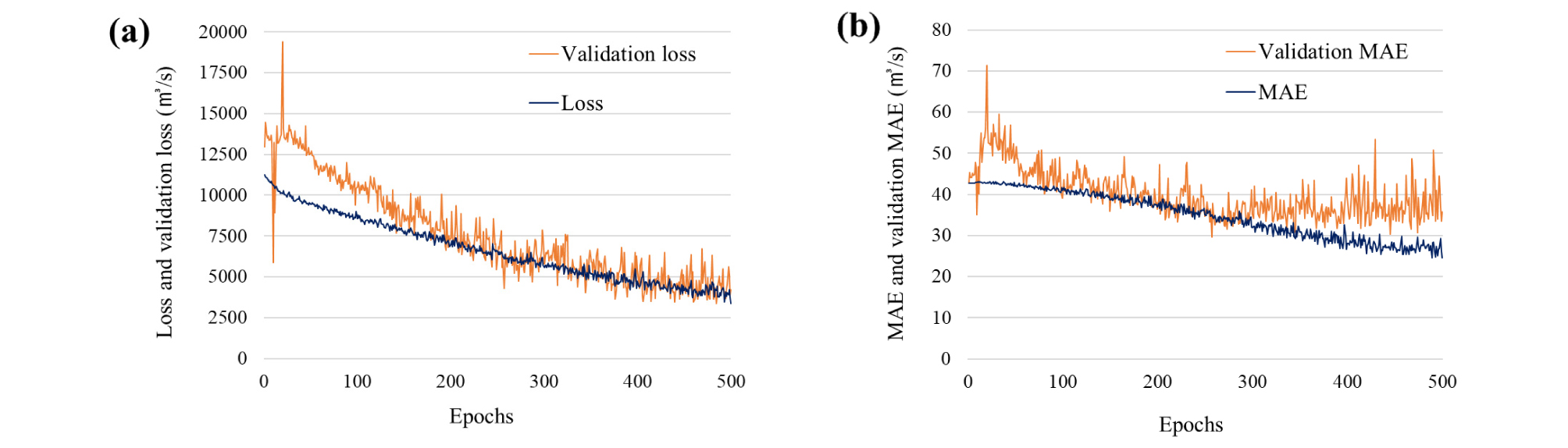
모형의 학습 결과는 Fig. 6과 같다. Fig. 6 (a)는 loss 및 validation loss, Fig. 6 (b)는 MAE 및 validation MAE를 나타낸다. 안정적으로 모형의 학습이 진행될 경우, loss, validation loss, MAE 및 validation MAE의 변화량은 밑수 (base)가 0 이하인 지수함수 그래프 형태와 유사한 형태로 진행된다.
Fig. 6 (a)의 경우, loss는 첫 학습횟수에 11,264.26으로부터 시작하여, 최종 학습횟수에 3,372.72까지 학습횟수가 진행됨에 따라 안정적으로 감소하는 것으로 나타났다. validation loss는 초반 불안정한 변화를 보였으나, 첫 학습횟수에 12,980.25로부터 시작하여, 최종 학습횟수에 4,199.01까지 학습횟수의 증가에 따라 점차 감소하는 것으로 나타나 모형의 학습 및 일반화가 안정적으로 진행된 것으로 판단하였다.
모형의 관측값과 산정값간의 오차 변화를 나타내는 Fig. 6 (b)의 MAE는 첫 학습횟수에 42.68로 시작하여, 최종 학습횟수에는 24.58까지 안정적으로 감소하였다. 이는 모형의 학습이 진행되면서 모형의 산정이 점차 관측값에 가깝게 모의되는 것을 의미한다. 이와 달리, validation MAE는 validation loss와 마찬가지로 학습횟수가 초반 증가하는 동안에 불안정한 변화를 보였으나, 학습횟수의 진행에 따라 점차 감소하는 것으로 나타났다. 다만, 250번째 학습횟수를 지나면서 불안정한 변동을 보였으나, 결국 validation MAE가 감소하는 형태로 나타나, 모형의 검정 단계에 대한 모형의 일반화가 진행된 것으로 판단하였다.
3.5 산정 결과 및 모형 평가
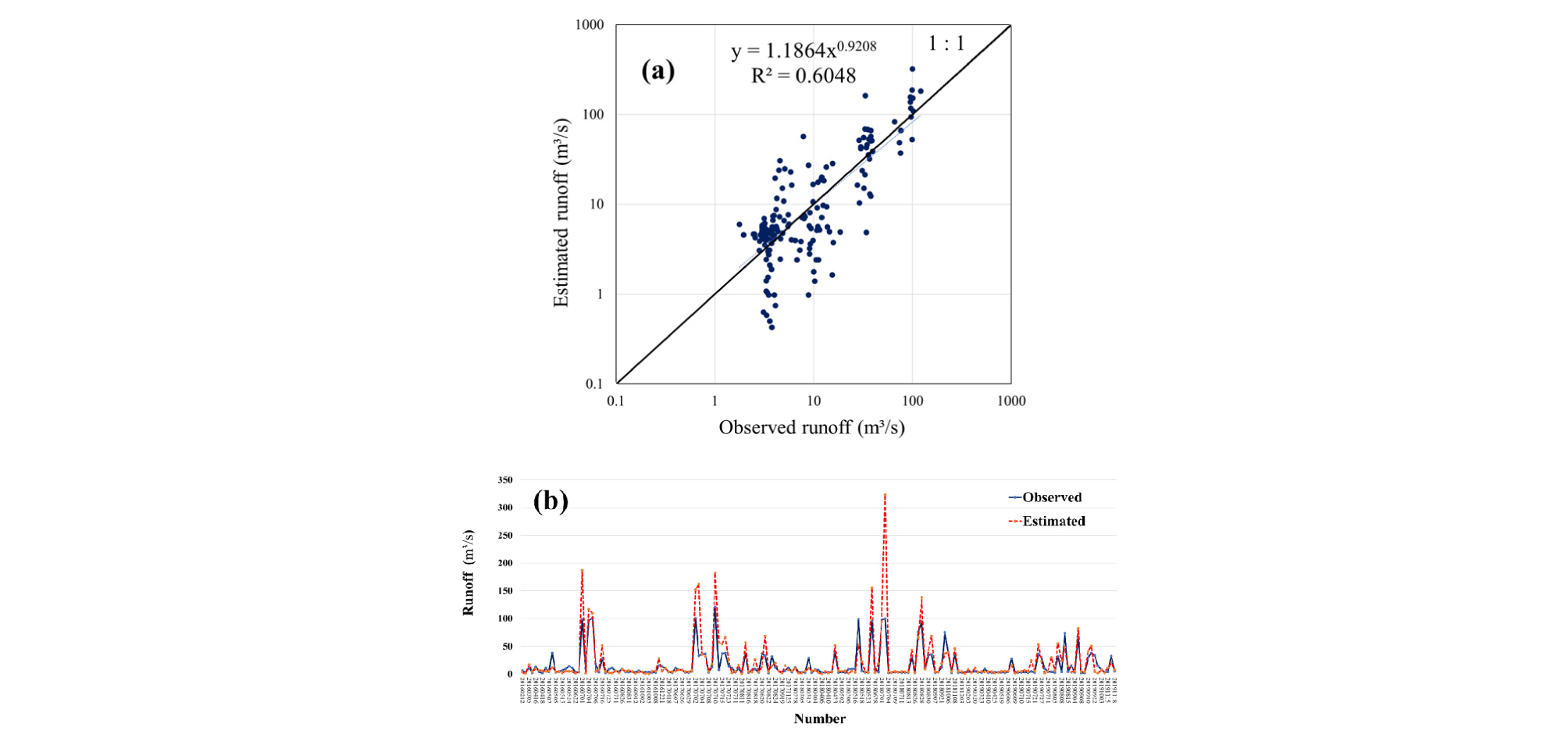
모형의 성능을 판단하기 위해 앞서 분류한 테스트 자료셋을 이용하였다. 모형의 산정값과 관측값에 대한 비교 결과를 Fig. 7과 같이 나타냈다. Fig. 7 (a)에서 가로축은 관측값을, 세로축은 산정값을 나타내며, 양축 모두 로그스케일로 나타냈다. 1:1 직선에 근접할수록 모형의 모의수준이 높은 것을 의미하는데, Fig. 7 (a)와 같이 관측값과 산정값에 관한 값이 1:1 직선 주변에 점들이 분포하고 있으나, 관측유량의 규모가 낮을 수록 1:1 직선 아래로 오차가 커져 과소추정되는 경향이 나타났다. 또한, Fig. 7 (b)와 같이 산정값과 관측값의 변화를 나타내었는데, x축은 테스트 자료셋의 이미지 개수를 나타내며, y축은 이미지에 의한 산정값과 관측값을 의미한다. 109번째 이미지의 산정값 (323.18 m3/s)가 관측값 (99.97 m3/s)보다 약 3배 이상 높게 산정된 것을 제외하면, 전반적으로 산정값과 관측값간의 변화경향이 유사한 것으로 나타났다.
모형을 평가하고자 앞서 언급한 바와 같이 r, NSE, 및 RMSE를 Table 4와 같이 나타냈다. Table 4에서 r은 0.84로 산정값과 관측값간의 선형성이 매우 높은 것으로 나타났다. NSE는 일반적으로 0.65 이상인 경우에, 모형이 우수한 성능을 갖는 것으로 판단하는데 (Moriasi et al. 2007), 본 모형의 NSE는 우수한 성능을 나타내는 기준에는 못미치는 0.63으로 나타나 모형의 성능이 준수한 수준으로 판단할 수 있다. RMSE는 24.54 m3/s으로, 모형의 최종 학습결과인 MAE 값 24.58과 유사한 것으로 나타났다. 이 처럼 CN, 강우 및 AMC 등의 조건을 고려하여 생산된 유역 이미지를 연속변수 모의가 가능하도록 수정된 CNN 모형의 입력자료로 사용한 모형의 평가는 전반적으로 양호한 상태의 훈련 결과와 산정 성능을 보인 것으로 나타났다.
4. 결 론
본 연구는 분류문제에만 사용되어 왔던 CNN을 연속변수 모의에도 사용하고자, CNN의 핵심 기능인 합성곱 층 및 풀링 층을 활용하여 이미지 특성을 추출할 수 있게 유지하였고, 완전 연결층을 수정하여 연속변수 모의가 가능하도록 하여, 우수한 결과를 나타냈다. 또한, 전통적으로 유출량 추정을 위해 사용된 CN 및 SCS 방법론이 모형의 입력자료인 이미지 생성을 위해 활용 가능함을 보였는데 특히, CN을 기반으로 한 이미지 생성이 가능함에 따라 새로운 CN의 용도를 제시할 수 있었다. 이와 함께, 기존의 유량 모의를 위해 주로 사용했던 DNN 활용에서 벗어나, 본 연구의 방법론을 통해 다른 신경망으로도 유량 모의가 가능하다는 것을 나타냈다.
그러나 본 연구와 같이 CNN을 활용한 유량모의 기술은 선행연구가 거의 없는 것과 같이 초기 기술 수준에 머무르는 것으로 판단되며 특히, 유량 모의를 위한 CNN 모형의 구조나 정확성 등과 같은 개선되어야 할 부분이 현저히 많아, 향후 본 연구의 후속 연구로 추진하고자 한다.
그럼에도, 본 연구에서 사용한 방법론이나 신경망 기술이 점진적으로 발전할 경우, remote sensing 분야에 접목되어 유량 모의 연구에 활용되거나, 위성영상을 이용하여 전 지구적 또는 광역 단위의 실시간 유량모의가 가능할 것으로 판단되는 등의 기술 활용범위가 매우 클 것으로 판단된다.