1. 서 론
2. 수치모형의 적용성 검토
2.1 수치모형의 특징
2.2 수치해석 기법
3. 수치모형의 적용
3.1 수치모의 조건
3.2 수치모형의 적용성 검토
4. 수제에 의한 하도의 안정성 평가 기법
5. 수치모의결과 평가
6. 결 론
1. 서 론
수제는 하천에서 흐름의 방향을 제어하고 하천제방 및 하안침식을 방지하기 위하여 설치하는 수공구조물이다. 또한 수제는 주운을 위한 주수로 수심확보, 하도 안정성 확보, 생태환경 개선 등 하천의 이수, 치수, 생태환경적인 측면에서 다양하게 활용되고 있다. 그러나 수제 주변에서 통수단면의 감소로 인하여 평균유속과 단위폭 당 유량이 증가하며, 수제 주변에서 발생하는 강한 와류에 의하여 수제 주변에 국부적인 세굴이 발생한다 (Yeo 2006). 이로 인하여, 하도 전체적으로 하상 및 지형변화를 일으키거나 국소세굴로 인한 구조물 자체의 안정성이 저하되기도 한다. 이와 같이 하도에서 수제를 계획하거나 설계 및 시공 단계에서 다양한 수리학적 특성과 하천의 지형학적 조건을 충분히 고려하여야 하지만. 현재까지는 현장 여건을 충분히 고려한 실용적인 설계기준이나 이에 대한 사후 평가방법이 개발되어 있지 않은 실정이다. 수제 설치를 통한 하안침식 방지 효과는 하천의 수리학적 특성 및 하천의 지형학적 형태 등에 따라 차이가 있을 수 있다. 따라서 수제 설치의 효율성을 높이기 위해서는 수제 설치에 따른 수리학적 특성뿐만 아니라 유사이송 및 만곡부의 특성과 같은 하천 형태에 대한 고려가 필요하다. 그러나 이러한 현상들은 매우 복잡하게 관련이 있을 뿐만 아니라 대상구간의 특성에 따라 변화하기 때문에 수제 설치로 인한 하도의 안정성을 평가하는 것은 쉽지 않은 일이다.
수제에 대한 연구는 수제의 길이, 설치각도의 변화 등에 따른 수제주변의 흐름과 하상 및 지형변화에 대한 연구가 주로 진행되어 왔다. Elawady et al. (2001)은 실험을 통해 흐름의 방향에 대하여 기울어진 수제의 흐름 및 세굴특성을 분석하였으며, 이러한 특성은 흐름에 대한 경사수제의 유효길이와 수제의 높이에 의해 영향을 받는 것으로 분석하였다. Nagata et al. (2005)는 수제 및 교각 주변에서 흐름 및 유사의 비평형특성을 고려한 국부적인 하상변동을 정교한 3차원 수치모형을 개발하여 분석하였으나, 하상변동을 예측함에 있어서 매개변수의 민감도 분석이 필요하다. Teraguchi et al. (2008)은 투과성 수제와 불투과성 수제 주변에서 난류의 거동과 하상변동 특성을 실내실험과 3차원 수치모의를 수행하여 분석하였다. Duan (2009)은 ADV (Acoustic Doppler Velocimetry)를 이용하여 수제 주위의 3차원 유속을 측정하고, 수제 직하류에서 순환흐름의 구조를 정량적으로 분석하였다.
Yeo et al. (2006)는 사각형 불투과 수제에 대한 흐름분리 영역과 흐름 중심선 영역을 실험을 수행하여 제시하고, 본류 흐름변화를 분석하였다. Kang et al. (2009)은 수제 선단부가 경사를 이루는 경사 수제를 대상으로 수제주변의 유속을 LSPIV (Large Scale Particle Image Velocimetry)기법을 이용하여 측정하였다. 특히, 수제 주변의 주흐름영역과 재순환영역의 흐름 특성을 분석하고, 경사 수제의 재순환영역에서 재순환 유속이 감소하는 것을 파악하였다. Lee and Jang (2016)은 2차원 수치모형을 이용하여 수제군이 설치되었을 때, 수제의 설치간격과 길이변화에 따라 흐름특성과 하도의 변화 과정을 분석하였다. 특히, 수제의 길이와 수제간 간격의 비를 나타내는 무차원 수제 간격이 4 - 10일 때, 군수제의 효과가 감소하는 것을 파악하였다. Jang and Song (2016)은 수제의 길이 변화에 의한 교호사주의 형성, 사주의 이동과 정지, 사주의 파장에 미치는 영향을 실내실험을 통하여 분석하였다.
이러한 연구들은 주로 수제 주변의 흐름구조와 수제 선단부에서 발생하는 국부세굴, 수제에 의한 사주의 거동과 저수로의 변화를 정량적으로 분석하였으나, 실제 현장에서 수제 설치에 의한 저수로의 안정성을 평가한 연구가 거의 없는 실정이다. 따라서 본 연구에서는 실제 현장을 대상으로 수제에 의한 하도의 안정성을 수리학적 특성을 반영하여 정량적으로 평가할 수 있는 기법을 개발하고, 2차원 수치모의를 수행하여 그 적용성을 검토하였다.
2. 수치모형의 적용성 검토
2.1 수치모형의 특징
Nays2DH모형은 직교좌표계를 일반좌표계로 변환하여 형상이 복잡한 하천을 모의하는데 적합하도록 하였다. 본 모형은 하천의 지형 및 수리구조물을 고려한 2차원 흐름특성을 계산하고, 하안침식과 식생의 영향을 고려한 하도 변화와 유사의 분급 현상을 모의할 수 있다 (Shimizu et al., 2014).
본 모형에서 2차원 흐름 거동을 모의하기 위한 흐름의 지배방정식은 수심적분된 연속 방정식 및 운동량 방정식을 이용하였다. 직교좌표계에서 일반좌표계로 좌표 변환한 지배방정식은 다음과 같다.
여기서 ξ와 η은 일반좌표계에서 공간 좌표 성분이며, uξ와 uη는 ξ와 η 방향의 유속이다. H는 수위 (=h+z)이고, h는 수심 (m)이며, z는 하상고 (m)이다. as는 단위체적당 식생에 의해 차단되는 단면적이며, CD는 식생에 의한 항력계수이다. CF는 하상마찰계수이고, n은 Manning의 조도계수이며, J는 Jacobian이다. 계수 α1 - α6는 다음과 같다.
위 식의 운동량 방정식에서 확산항 Dξ와 Dη는 다음과 같이 표현할 수 있다.
| $$D^\xi\cong\frac\partial{\partial\xi}\left(\nu_t\xi_r^2\frac{\partial u^\xi}{\partial\xi}\right)+\frac\partial{\partial\eta}\left(\nu_t\eta_y^2\frac{\partial u^\xi}{\partial\eta}\right)$$ | (5a) |
| $$D^\eta\cong\frac\partial{\partial\xi}\left(\nu_r\xi_x^2\frac{\partial u^\xi}{\partial\xi}\right)+\frac\partial{\partial\eta}\left(\nu_t\eta_y^2\frac{\partial u^\eta}{\partial\eta}\right)$$ | (5b) |
여기서 Dξ와 Dη는 ξ와 η에 대한 확산항이며, ξr와 ηr는 일반좌표계에서 격자의 크기와 국소적인 격자의 크기 비를 나타낸다.
Nays2DH 모형에서는 난류에 대한 문제를 해결하기 위하여 zero 방정식을 적용하였다. 하상마찰속도와 수심 지배적 운동량 이송을 고려한 와동점성계수 νt는 다음과 같다.
| $$\nu_t=au_\ast h$$ | (6) |
여기서 α는 비례상수로서 실험에 따라 수직방향의 운동량이송에 관련된 값으로 약 0.07이다. 일반좌표계에서 2차원 유사의 연속방정식은 다음과 같다.
여기서 zb는 하상고이고, λ는 하상재료의 공극률이다. 와 는 ξ와 η방향에 대한 단위폭당 소류사량이며, J는 Jacobian이다. 유사량은 Ashida and Michiue (1972)의 공식으로 계산하였으며, 다음과 같다.
| $$q_b=17\tau_\ast^{3/2}\left(1-\frac{\tau_{\ast c}}{\tau_\ast}\right)\left(1-\frac{u_{\ast c}}{u_\ast}\right)\sqrt{{\mathrm s}_{\mathrm g}\mathrm{gd}^3}$$ | (8) |
여기서 qb는 소류사량 (m3/s/m)이며, sg는 수중에서 하상토의 비중이다. g는 중력가속도 (m/s2)이고, d는 하상토의 평균입경 (mm)이다. 는 무차원 소류력이며, 는 무차원 한계 소류력이다. 는 마찰속도 (m/s)이고, 는 한계 마찰속도 (m/s)이다.
2.2 수치해석 기법
수치해석 기법으로 엇갈린 격자 (staggerded grid) 상에서 이류항에는 CIP (Cubic Interpolated Pseudoparticle)법을 적용하였으며, 확산항에는 중앙차분법을 적용하였다. 경계조건으로 상류에는 유량과 유사량을 설정하였으며, 하류에는 등류수심을 설정하였다. 측벽에서는 측벽에 유속이 없는 것으로 가정하여 비활동 조건 (No slip)을 적용하였다.
3. 수치모형의 적용
3.1 수치모의 조건
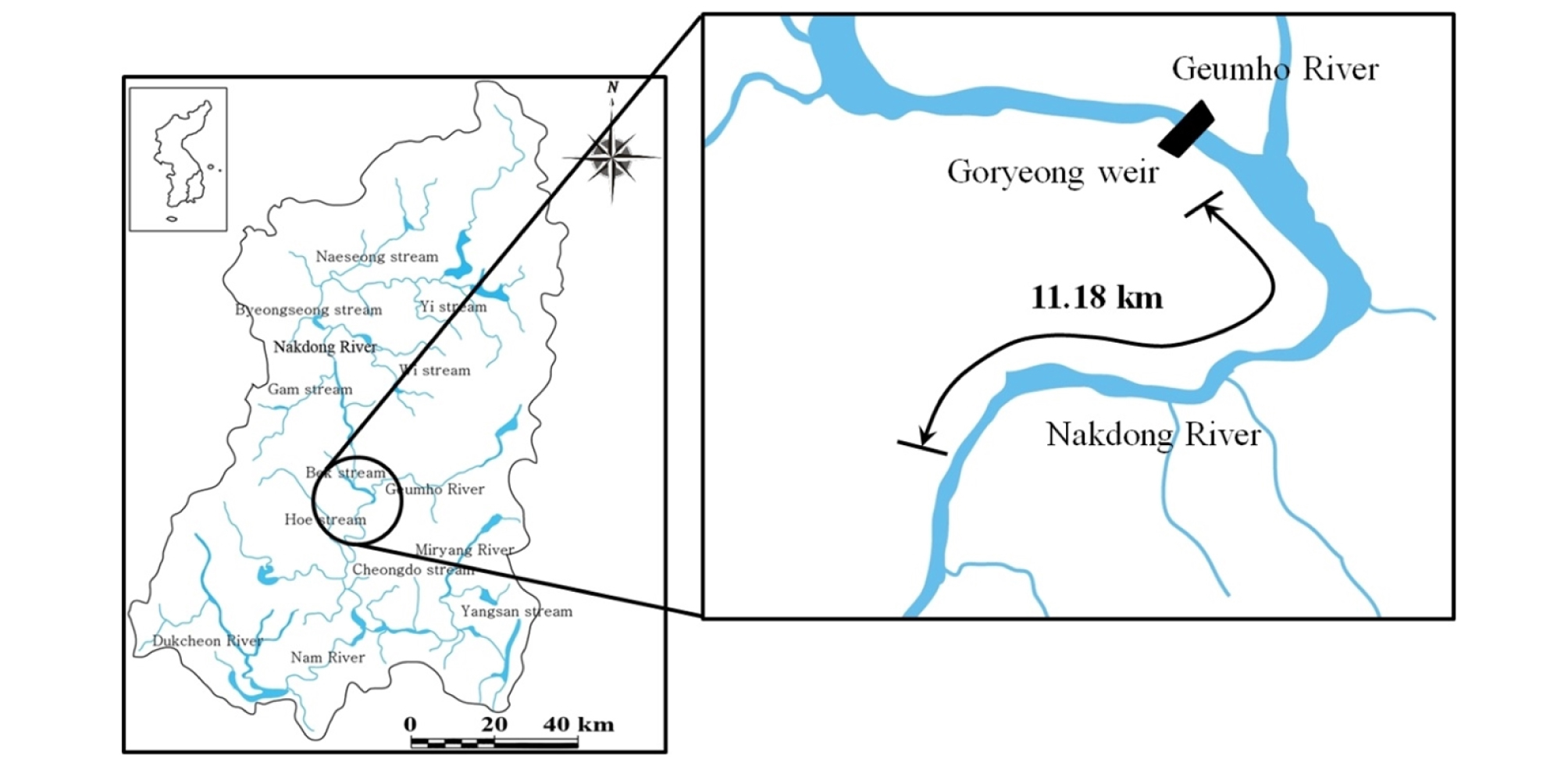
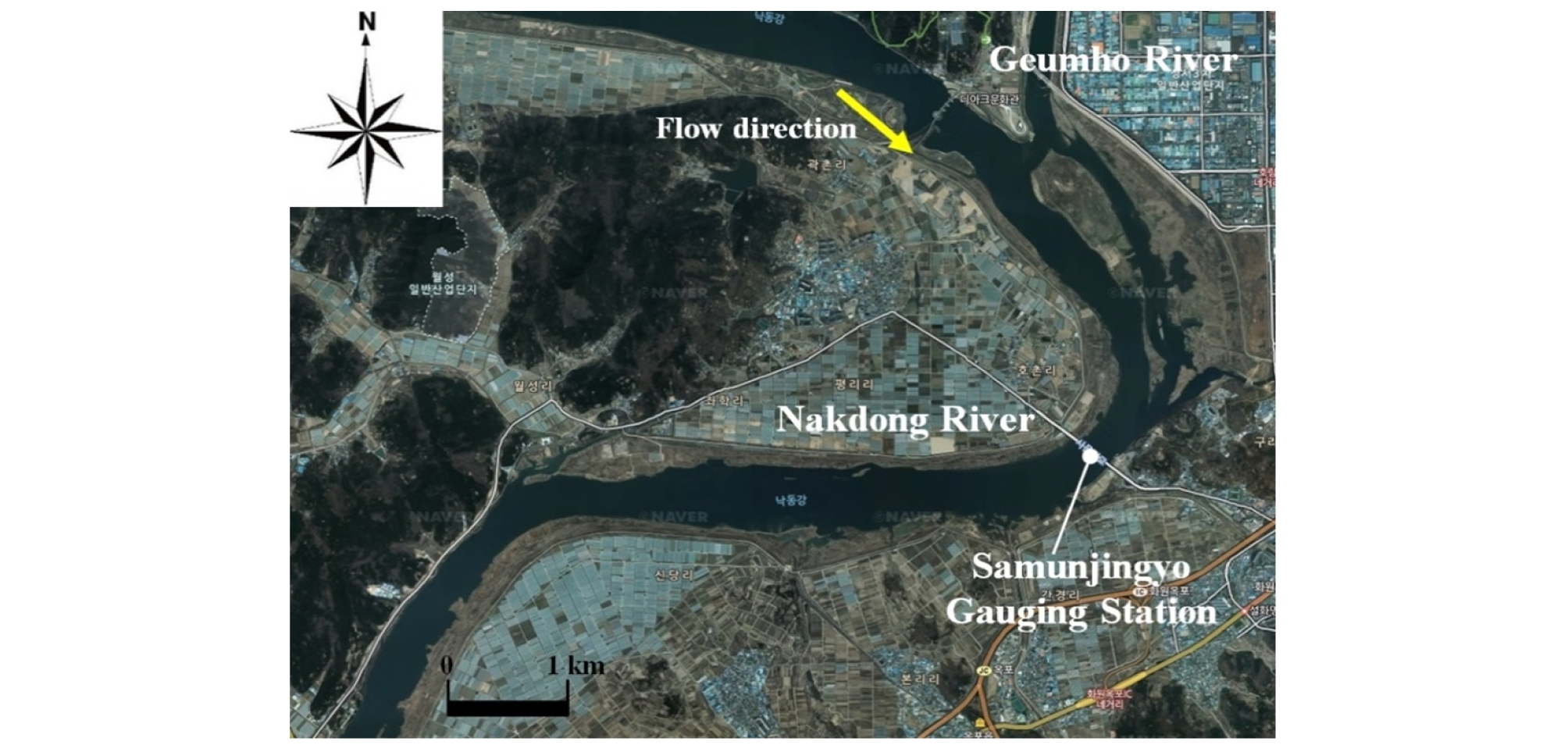
연구 대상 유역은 대구광역시 달성군 다사읍 죽곡리에 위치한 강정고령보를 대상으로 하류 11.2 km 구간을 선정하였다 (Fig. 1). Fig. 2는 대상구간의 위성사진을 나타낸다. 강정고령보로부터 약 1 km 하류에서 좌안에 금호강이 합류하고 있고, 낙동강과 금호강이 합류하는 지점에서 하중도가 발달되어 있다. 합류부 하류로는 우안을 내측으로하는 만곡부가 형성되어 있다. 수치모의를 위하여 지형자료는 하도단면은 2012년에 실측된 자료를 이용하였다. 대상 구간의 하상경사는 0.0004이며 상대적으로 완만하다. 하상토의 평균입경은 5.875 mm이며, 하상은 가는 자갈로 구성되어 있다. 대상구간 에서 Manning의 조도계수 (n)는 낙동강 하천정비기본계획 (MLIT, 2013)에서 제시한 0.023을 적용하였다.
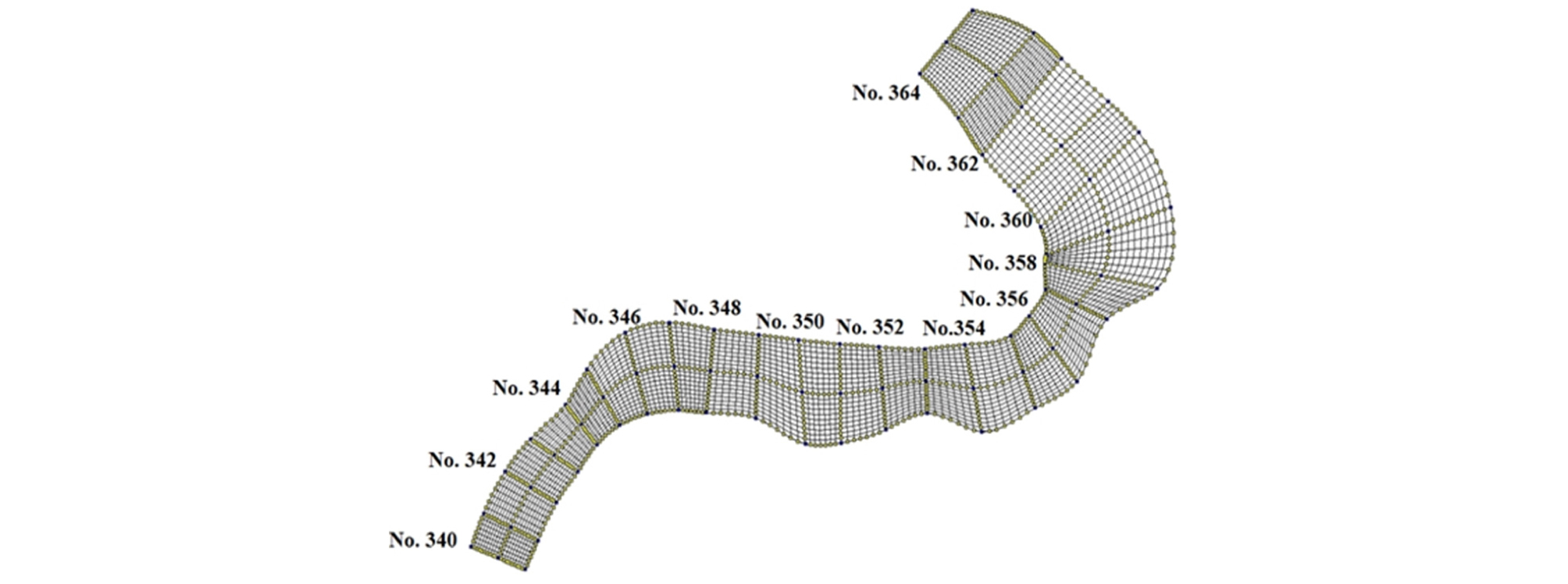
부정류 수치모의를 위한 유량자료는 낙동강 하류에 위치한 사문진교 수위관측소의 2012년 9월 15일부터 2012년 9월 20일까지 시간별 관측 자료를 적용하였다. 이때, 최대 유량은 6,848.2 m3/s이며 최소유량은 728.6 m3/s이다. 수치모의를 위한 계산 시간 간격은 수치적 안정성을 확보하기 위하여 1초로 설정하였다. 계산 격자 크기는 흐름방향 (Dx)으로 평균 65 m이며, 횡방향 (Dy)으로 평균 30 m로 적용하였다 (Fig. 3 and Table 1).
Table 1. Numerical simulation conditions
| Parameter | Unit | Value |
| Channel length | km | 11.18 |
| Bed slope | 0.0004 | |
| Mean diameter of sediment | mm | 5.875 |
| Manning n value | 0.023 | |
| Time step | Seconds | 1 |
| Run time | Hours | 144 |
| Calculation grid size | Dx × Dy | 65 m × 30 m |
3.2 수치모형의 적용성 검토
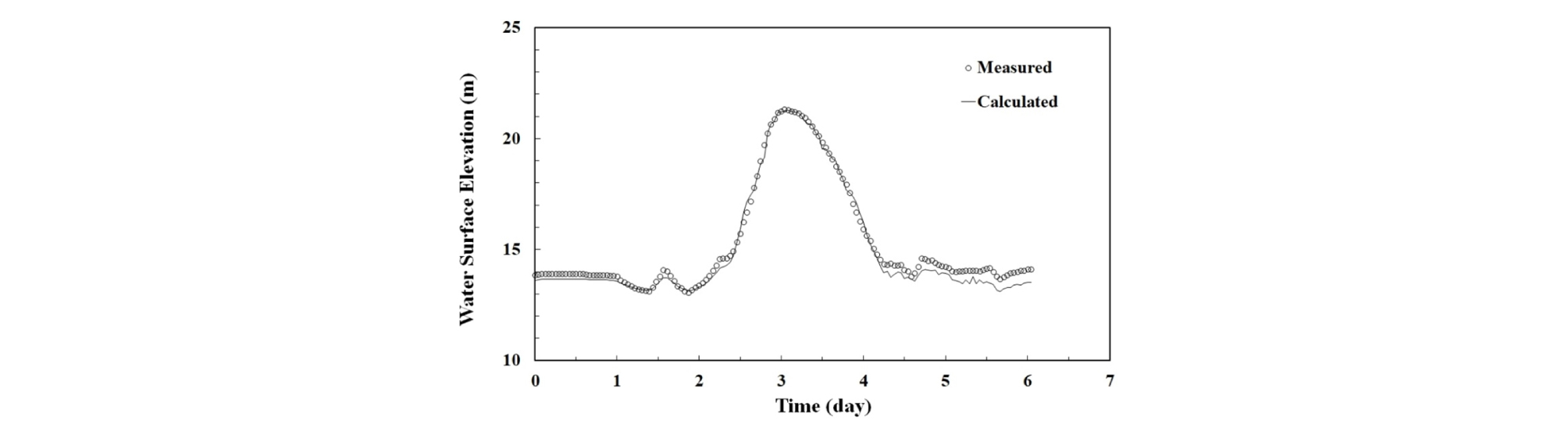
2차원 수치모형의 부정류에 대한 적용성을 검토하기 위하여 사문진교 수위표에서 관측된 시간에 따른 홍수위 변화와 수치모의 결과를 비교하였다. 사문진교 수위표에서 홍수위는 2012년 9월 15일 00시부터 2012년 9월 20일 24시까지 관측결과이다. 첨두홍수위는 수위표에서 관측된 결과와 수치모의 결과가 잘 일치하였다. 그러나, 홍수위가 저하되는 9월 18일부터 9월 20일에 수치모의 값은 관측값보다 상대적으로 작게 나타났다 (Fig. 4). 이는 저수위에서 계산격자를 구성함에 있어서 저수로의 미세한 지형변화를 반영하는데 한계가 있기 때문으로 판단된다.
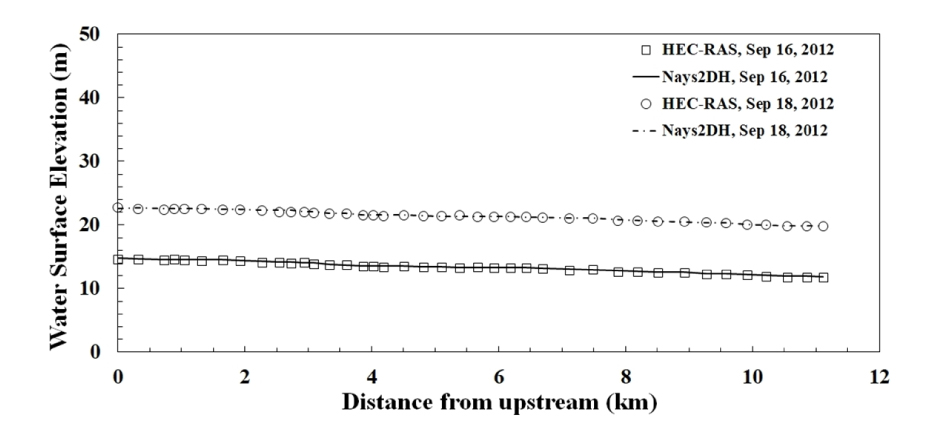
종방향 수위 변화인 부등류에 대한 수치모형의 적용성을 파악하기 위하여 2012년 9월 16일에 발생한 최소유량인 728 m3/s과 2012년 9월 18일에 발생한 최대유량인 6,848 m3/s를 적용하여 1차원 수치모형인 HEC-RAS 모형과 2차원 수치모형인 Nays2DH 모형과의 수치모의 결과를 비교하였으며 (Fig. 5), 모의 결과는 잘 일치하였다.
수치모의 결과를 정량적으로 분석하기 위하여, NSEC (Nash-Sutcliffe Efficiency Coefficient)와 RMSE (Root Mean Square Error)를 비교하였다. NSEC는 수치모의 결과의 정확성을 검증하는데 주로 사용되는 값이다. NSEC는 관측값의 분산으로 정규화 된 예측값과 관측값 사이의 절대 제곱 차이의 합에서 1을 뺀 것으로 정의되며, Eq. 9와 같다.
| $$\mathrm{NSEC}=1-\frac{\sum({\mathrm Q}_{\mathrm o}-{\mathrm Q}_{\mathrm m})^2}{\sum({\mathrm Q}_{\mathrm o}-{\overline{\mathrm Q}}_{\mathrm o})^2}$$ | (9) |
여기서 Qo는 측정값, 는 측정값의 평균, Qm은 모의결과이다. NSEC가 1이면 측정값과 모의결과가 일치하는 것을 의미한다.
평균제곱근 오차를 나타내는 RMSE는 측정값과 모의값의 오차를 정량화하여 나타내는 지표로 0에 가까울수록 측정값과 유사하다는 것을 의미한다. 모델이 예측한 값과 실제 환경에서 관찰되는 값의 차이를 다룰 때 사용되는 척도이며, 정밀도를 표현하는데 적합하다. RMSE를 나타내는 산정식은 Eq. 10과 같다.
| $$\mathrm{RMSE}=\frac{\sqrt{\sum({\mathrm H}_{\mathrm o}-{\mathrm H}_{\mathrm m})^2)}}{\mathrm n}$$ | (10) |
여기서 Ho는 측정값, Hm은 수치모의값이다.
관측 값과 2차원 수치모의 결과를 비교 분석한 결과, NSEC는 0.997, RMSE는 0.212로 나타났으며, 관측값과 모의값이 잘 일치하는 것으로 나타났다 (Table 2). 또한 2차원 모형의 적용성 검토를 위해 1차원 수치모형인 HEC-RAS와 흐름에 대한 모의결과를 비교하였다. NSEC는 0.985 - 0.987로 분석되었으며, RMSE는 0.086 - 0.105로 분석되었다. 따라서, 1차원 수치모형의 모의결과와 2차원 수치모형의 모의결과가 잘 일치하는 것으로 나타났다 (Fig. 5).
Table 2. NSEC and RMSE for numerical results
| Case | NSEC | RMSE | Remarks |
| 2D numerical result and observation for unsteady flow | 0.997 | 0.212 | Fig.4 |
| 1-D and 2-D numerical results for non-uniform flow | 0.985~0.987 | 0.086~0.105 | Fig.5 |
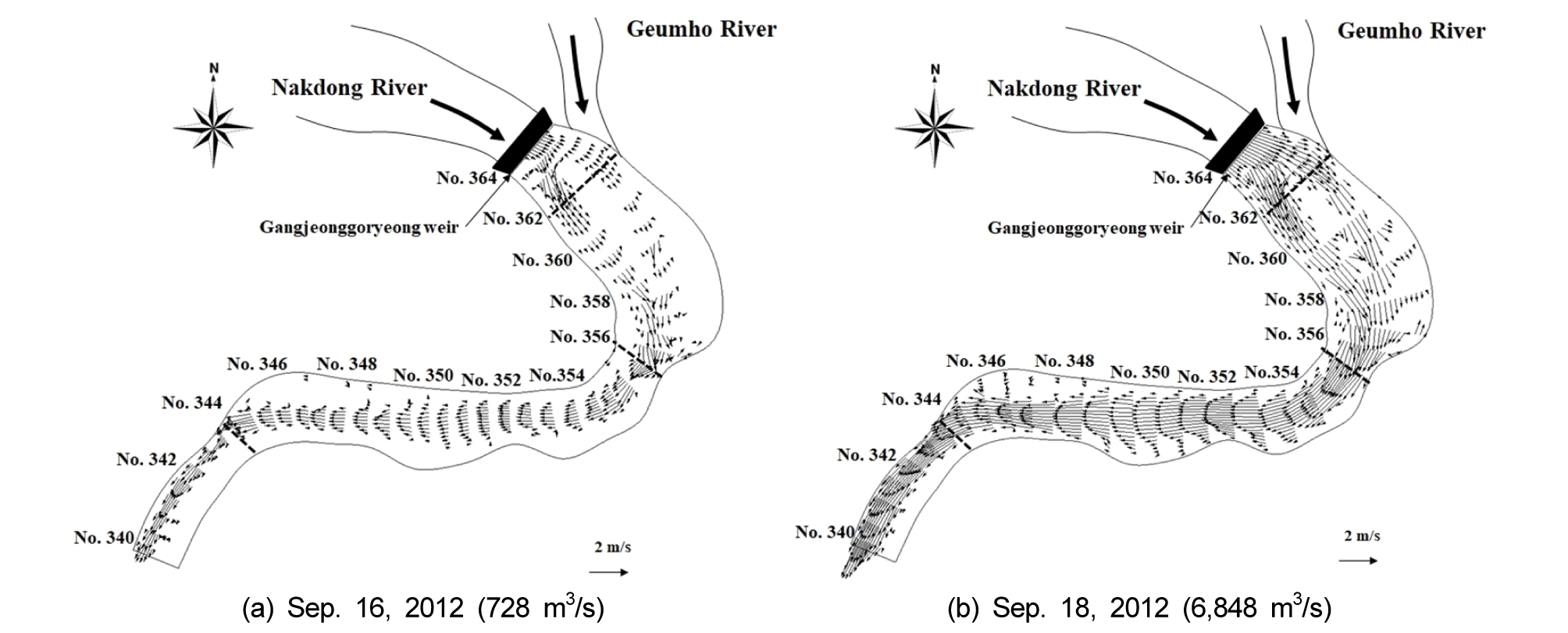
Fig. 6은 2차원 수치모형으로 계산된 유속분포를 보여주고 있다. 흐름은 강정보 하류에서 발달된 하중도에 의하여 보 직하류에서 흐름이 분리되었으나, No.358 지점에서 흐름이 다시 합류되었다. No.358 지점에서부터 No.354 지점까지 만곡부 외측인 좌안으로 흐름이 집중되었다. 유량이 6,848 m3/s일 때, 좌안에서 역류되는 와류가 형성되며, 만곡부의 유입부인 No. 358 지점에서는 우안으로 흐름이 집중되었다 (Fig. 6(b)). 그러나 유량이 728 m3/s일 때, 좌안에서 흐름이 저수로에 집중되고, No. 356 지점에서는 하도의 중앙에 흐름이 집중되었다. No. 358 지점에서는 저유량과 홍수량의 경우 모두 만곡부 외측인 좌안에 흐름이 집중되고 수충부를 형성하였다. 직선구간인 No.354 지점부터 No.348 지점까지의 구간에서는 흐름이 하도 중앙으로 집중되었다. 하류인 No.348 지점부터 No.340 지점까지의 구간에서는 만곡부 외측인 우안으로 집중되고, 수충부를 형성하였다.
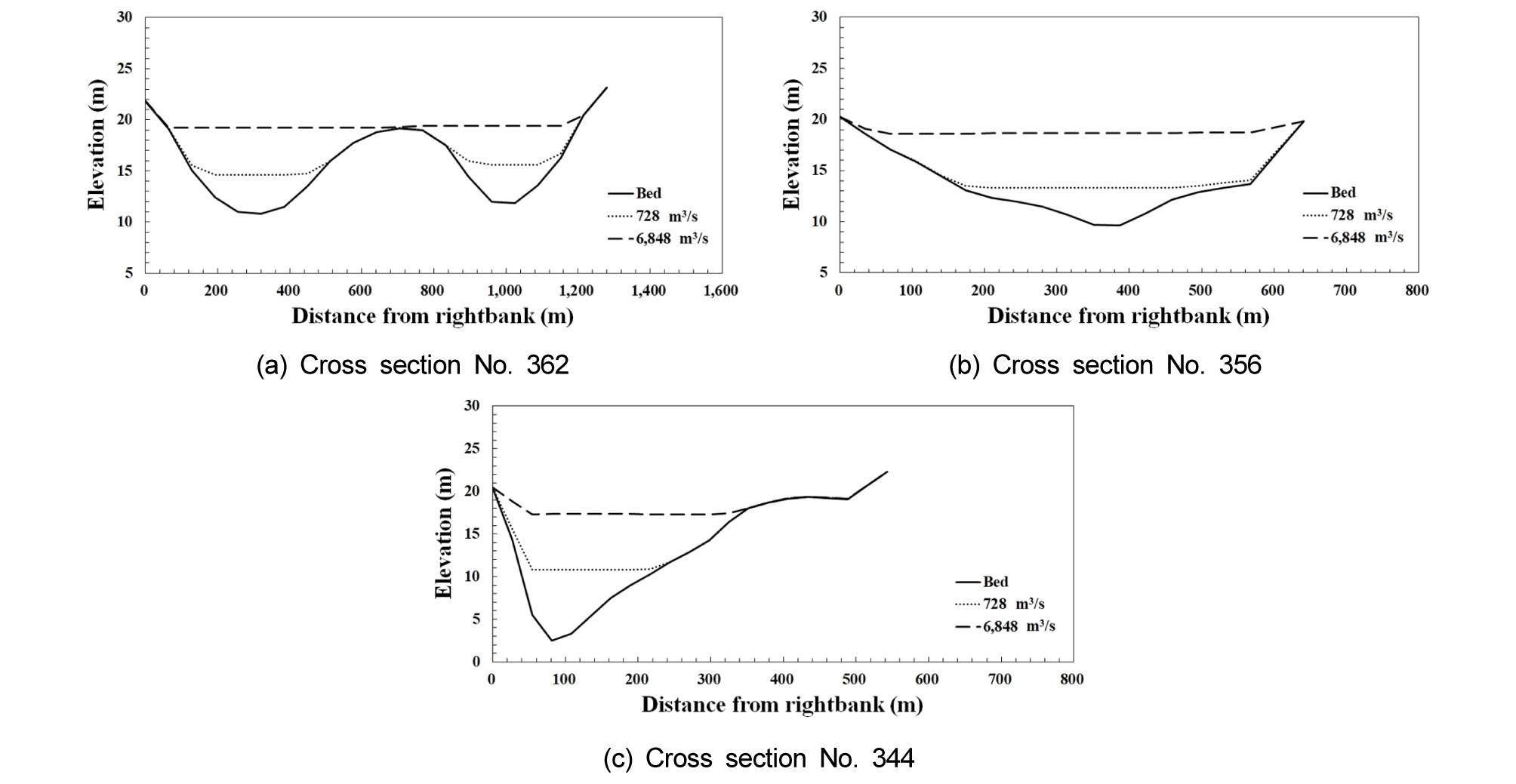
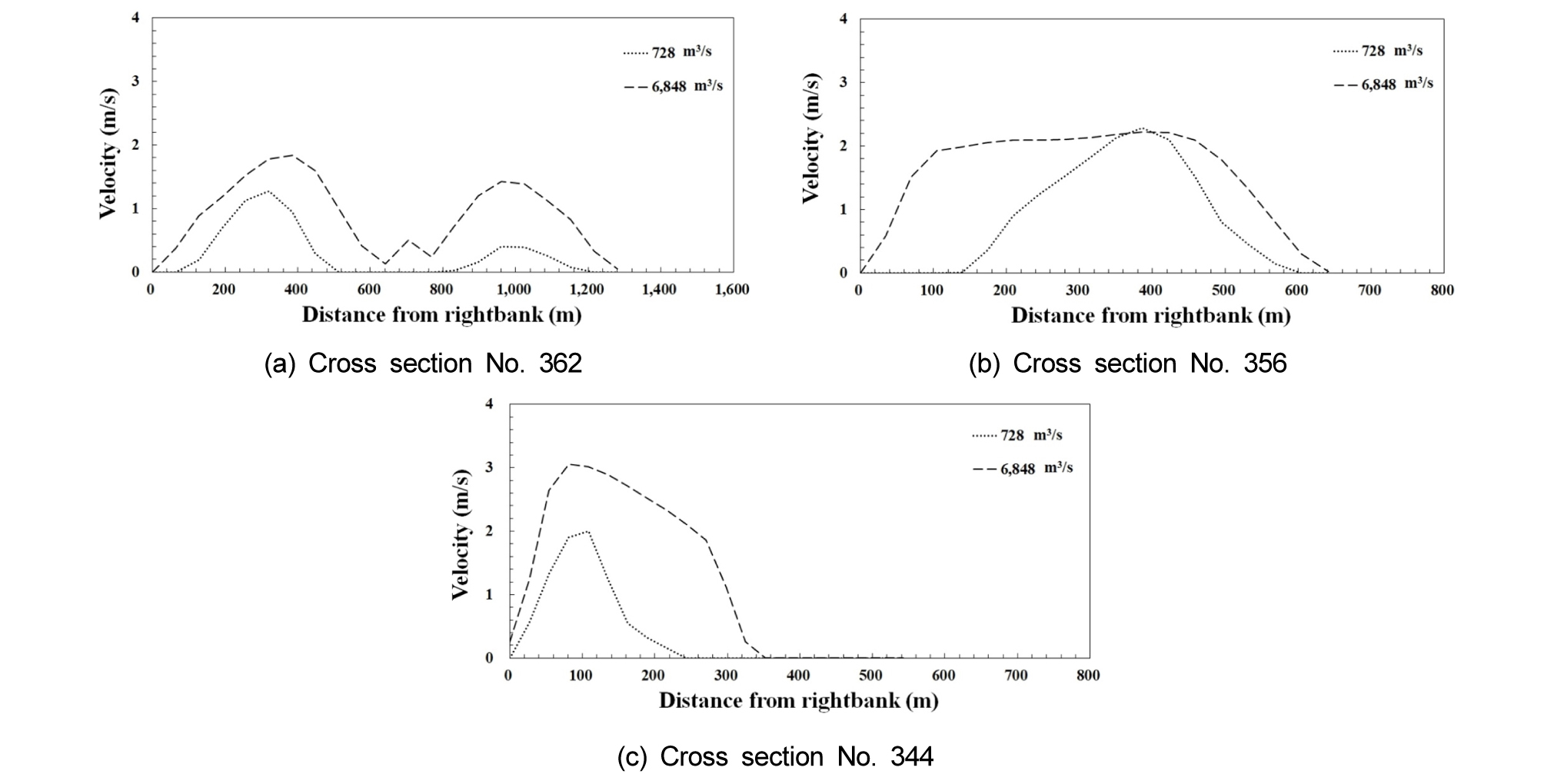
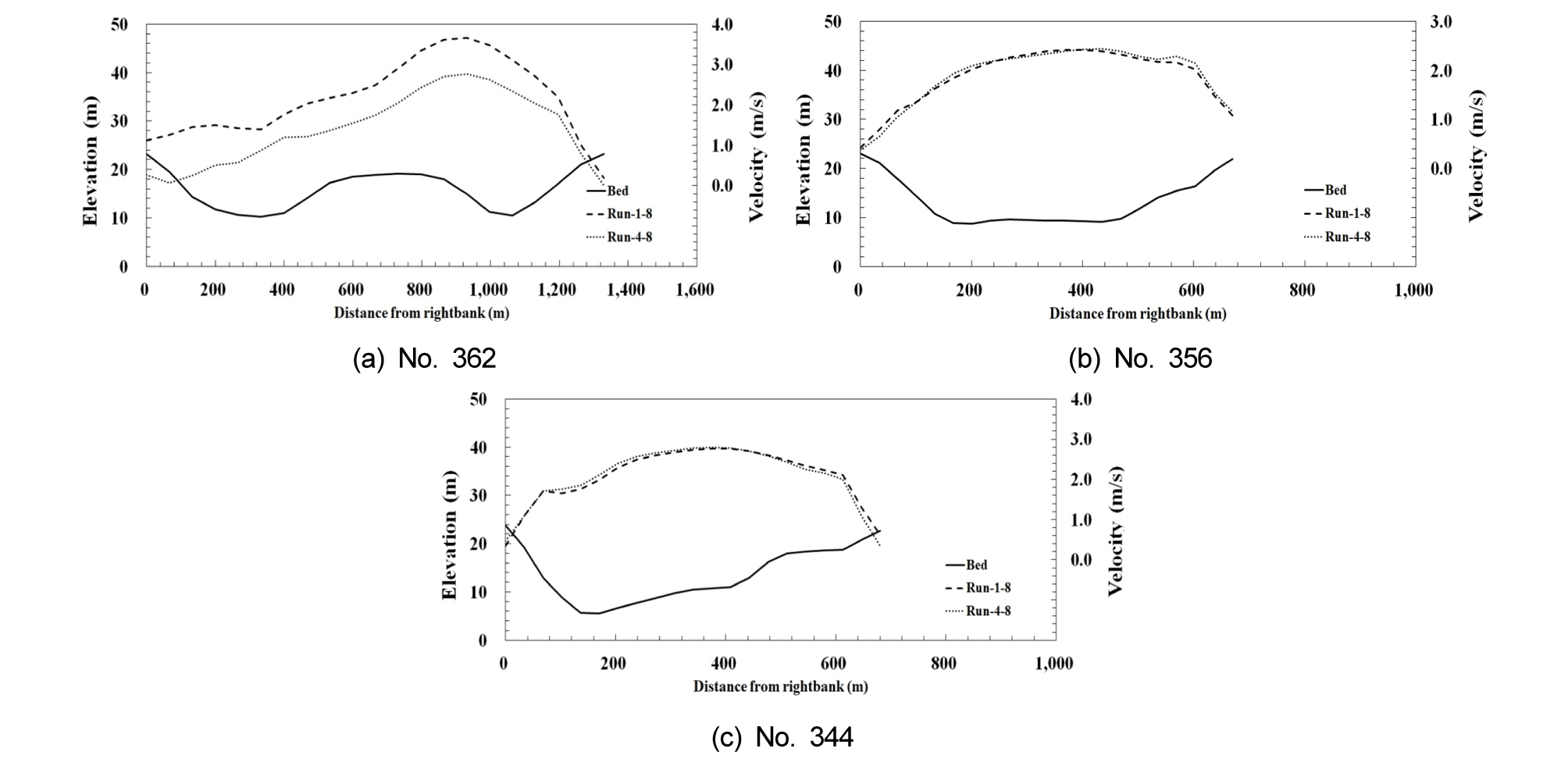
대상구간의 수심과 유속 분포를 정량적으로 파악하기 위하여 주요지점에서 횡방향 수심과 유속분포를 파악하였다 (Figs. 7 and 8). 하중도가 발달된 구간 횡단면인 No.362 지점에서 최소유량인 728 m3/s과 최대유량인 6,848 m3/s일 경우에 대해 수치모의 결과를 비교하였을 때 약 4.1 m의 수위차가 발생하였으며, 평균유속은 약 0.59 m/s의 차이가 발생하였다 (Figs. 7(a) and 8(a)). 좌안이 외측인 만곡부 No.356 지점에서 좌안으로 수심이 깊게 형성되고 있으며, 만곡부 외측으로 흐름이 집중되었다 (Fig. 7(b)). 만곡부의 횡방향 유속분포는 우안보다 좌안에서 유속이 빠르게 나타났으며, 기간 내 최대유량이 흐를 때 최대 유속은 2.22 m/s 이다 (Fig. 8(b)). 만곡부 외측에 수심이 깊으며 수충부를 형성하고 있다. 이러한 특성은 만곡부에서 강한 2차류의 영향을 받아 형성된 것이다. No.344 지점은 대상구간 하류에 해당하며 우안이 외측인 만곡부를 형성하고 있으며 (Fig. 8(c)), 최대유량과 최소유량일 때 3.6 m의 수위차가 발생하였다. 최대유량이 흐를 때 유속은 만곡부 외측인 우안에서 2.98 m/s로 가장 크게 나타났다 (Fig. 8(c)).
4. 수제에 의한 하도의 안정성 평가 기법
하도의 안정성 평가 기법을 개발함에 있어서 평가 지표는 하도 및 하안의 형태, 흐름 상태, 횡단면 형상 등을 종합적으로 고려하여 선정해야 한다. 특히, 하천에서 사주의 발달과 이동은 수충부를 형성하는데 중요한 지표이며, 이를 결정하는 데에는 하폭 대 수심의 비와 사행도를 고려해야 한다. 하폭 대 수심비가 상대적으로 크면, 복별사주가 발생하고 망상하천이 형성하며 하도의 불안정성이 증가한다. 그러나 하폭 대 수심의 비가 상대적으로 작으며, 교호사주가 발생하거나 사주가 발생하지 않는다. 본 연구에서는 Kuroki and Kish (1984)가 제안한 사주의 영역구분을 기준으로 토대로 하폭 대 수심의 비 값을 평가 지표로 설정하였다. 사행도는 하천의 사행을 나타내는 지표로써 하천의 최심선 길이와 직선거리의 비로서 표시된다 (Woo, 2011). 하상경사의 변화는 하상고 변화에 영향을 미치며, 홍수시 수면경사에 중요한 영향을 미친다. 하안 부근에서 유속은 수충부 형성 및 하안침식에 영향을 준다. Shields number는 양력과 중력의 비인 무차원 소류력을 나타내며, 유사이송량을 결정하는 지표로써, 다음과 같이 정의할 수 있다.
| $$\frac{u_\ast^2}{sgd}=\frac{hi}{sd}$$ | (11) |
여기서 는 마찰속도 (m/s)이고, s는 수중유사의 비중이다. d는 사립자의 입경 (mm)이고, g는 중력가속도 (m/s2)이다. h는 수심 (m)이고, i는 하상경사이다.
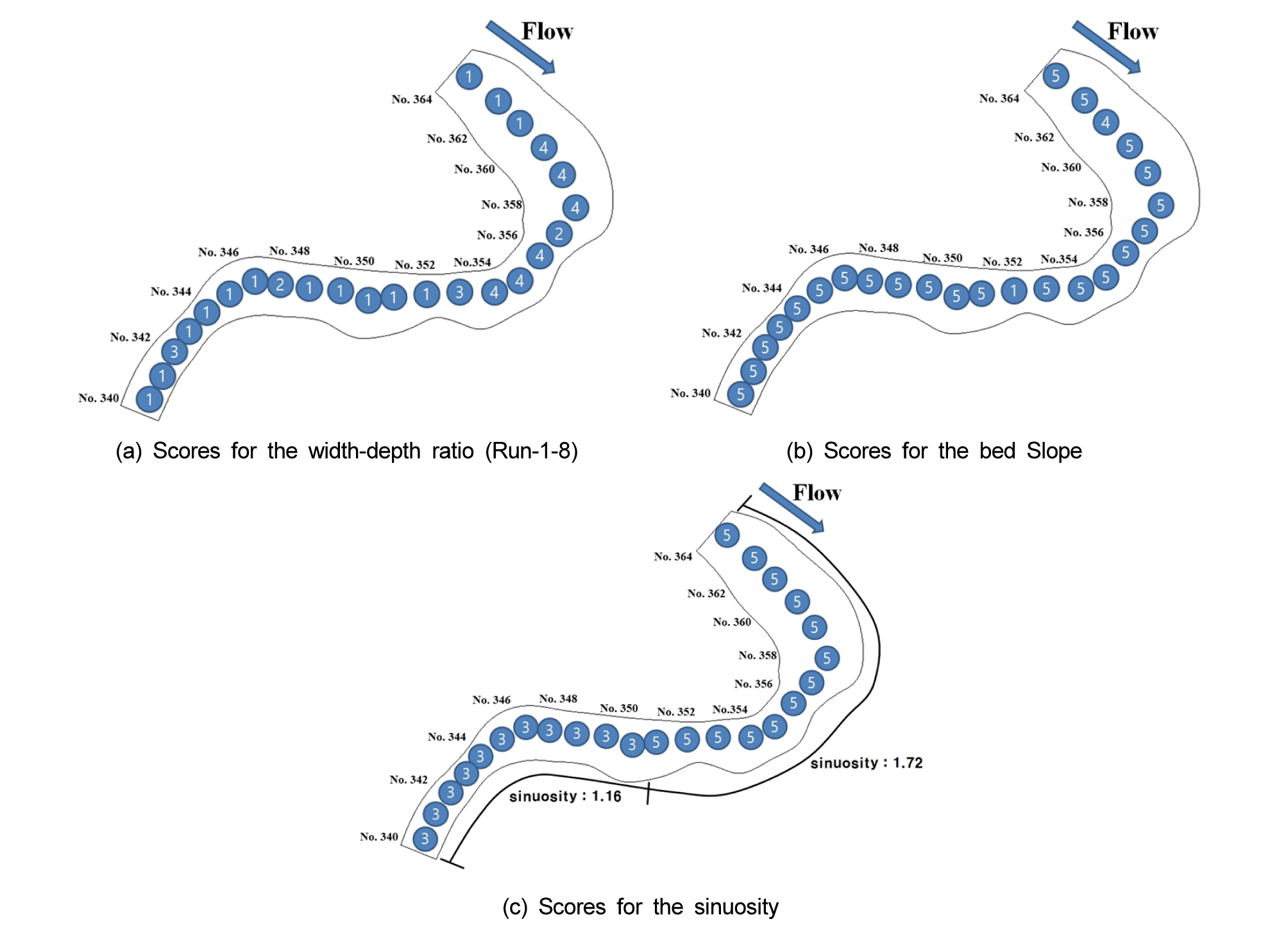
저수로 안정성 평가를 위한 평가항목은 하폭 대 수심의 비, 사행도, 하상경사, 하안 부근에서 유속, Shields number 등 5가지 항목으로 구성하였다 (Table 3). 평가항목으로 선정된 지표들을 표준화하기 위한 방법으로는 순위매기기, Z-score, re-scaling, Likert 척도법 등 여러 방법이 있으며, 이 중 순위매기기는 가장 단순한 방법이나 객관적으로 판단하기 힘든 방법이다 (Lee et al., 2016). Z-score법은 가장 보편적으로 사용되는 표준화 방법이며, 모든 자료의 평균을 0, 표준편차를 1이 되도록 만드는 방법이다 (Lee et al., 2016). Re-scaling법은 Z-score와는 다르게 지표의 범위를 고려한 변환방법이며, 이 방법은 지표들을 모두 동일하게 0 - 1사이의 범위를 갖게 하지만, 자료의 극값에 의해 지표에서 왜곡된 효과를 줄 수 있다 (Yang, 2012). Likert 척도법은 여러 개의 구성요소들 중 각 개념의 응답 값들의 총합으로 측정하는 방법으로써, 각 문항은 모두 비중이 같은 것으로 가정하고 총합을 단순 합산한 값으로 평가하는 방법이다. 사용이 용이하고 일관성이 있어 신뢰도가 높고 단순하며, 정밀성이 높으며 타당도가 높은 장점이 있다 (Kim, 2001). 본 연구에서는 분석의 용이성을 위해 Likert 척도법을 이용하였다. 대상유역에 대해 설정한 항목별 평가기준을 이용하여 지수화 한 후, 대상유역 구간에 대해 평가등급을 부여하였다. 각 항목에 대한 상세한 평가 기준은 Table 3과 같다.
Table 3. Variables and Grades for evaluation of the channel stability
Likert 척도법을 이용한 평가항목 별 가중치는 1점에서부터 5점까지를 5점 척도법으로 설정하였다. 점수의 위계는 치수적으로 유리한 경우에는 1점, 불리한 경우에는 5점을 부여하였다. 하도 내 사주의 형태는 하폭 대 수심비의 영향을 많이 받는다. 하폭대 수심비의 평가 항목은 구간 내 사주의 발생조건에 따라 사주가 발생하지 않는 조건, 교호사주가 발생할 조건, 복렬사주가 발생할 조건으로 구분하였다. 사행도에 대한 평가 항목은 구간 내 하도가 사수역, 직선부, 만곡부를 포함하는지의 여부에 따라 점수의 위계를 구분하였다. 하도에서 사수역이 형성되는 구간은 유사의 퇴적이 발생한다. 직선부는 수충부가 형성되지 않으며, 완만한 흐름을 나타낸다. 만곡부 외측은 수충부가 형성되며, 소류력이 크고 하안침식이 발생할 수 있는 구역으로써, 하도의 불안정성이 나타는 구간이다. 하상경사는 완경사 (1/3000 미만)의 조건부터 급경사 (1/200 이상)조건의 경우로 5개의 등급으로 구분하였다. 유속은 0.5 m/s 이하의 조건부터 3.0 m/s이상의 조건에 대하여 5개의 등급으로 구분하였다. Shields number는 무차원 소류력을 타나내며, 유사의 이동 특성을 나타낸다 (Eq. 11). 유사가 이동하기 시작하는 한계 무차원 소류력인 0.05를 기준으로 그 이하의 조건부터 0.2 이상의 조건에 대하여 5개의 등급으로 구분하였다.
하도 안정성 평가방법은 수치모의 결과에 대하여 Table 3에서 제시한 저수로 안정성 평가 기준을 적용하여 하도 구간별 저수로 안정성 평가를 수행한다. 또한 현장 조사를 통해 확인된 결과를 비교・검토하고, 이를 반영하여 위험도 구간을 설정한다 (Table 4). 저수로 안정성 평가를 수행하여 도출한 결과, 위험도를 1 - 5 등급으로 구분하고 등급 (평가값)이 높을수록, 저수로 안정화 대책이 시급한 구간으로 지정하고 관리하며 경우에 따라 저수로 안정화를 위한 비구조적인 대책과 병행하도록 해야 한다.
Table 4. Grades for Channel stability with scores and channel states
5. 수치모의결과 평가
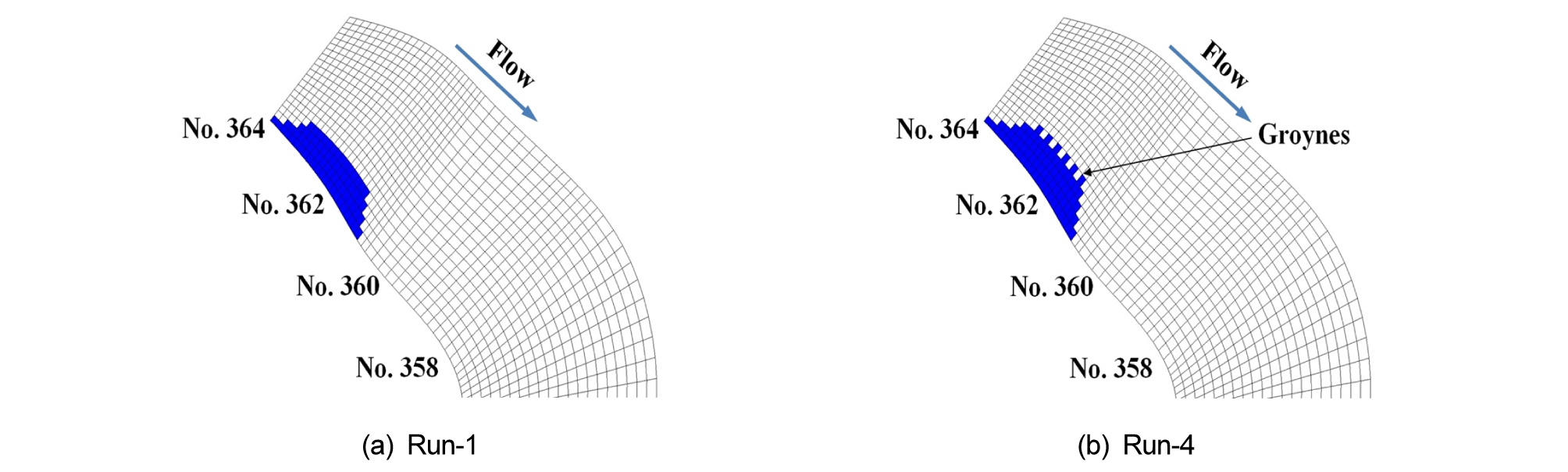
하도 안정성 평가지표를 실제 하천에 적용하기 위하여, 낙동강 본류인 달성보 (No.340)에서부터 강정고령보 (No.364)까지의 구간을 적용대상으로 하여, 2차원 수치모의를 수행하여 홍수빈도별 흐름특성 및 하도변화를 분석하였다. 수제에 대한 하도의 안정성을 평가하기 위하여 수제 설치 전‧후의 수리학적 영향을 분석하였다. 수치모의를 위한 수리학적 조건은 Table 5와 같다. 또한 강정고령보 하류의 지형학적 특성을 고려하고 수제에 의한 하도의 안정성 평가를 위하여 수제의 길이는 45 m, 간격은 35 m로 설정하였으며, 계산 격자는 Fig. 9에서 보여주고 있다.
Table 5. Numerical conditions for channel stabilities with groynes
Table 3은 하도 안정성 평가를 위한 각 항목별 등급 기준을 나타내며, Fig. 10은 Run-1에 대한 평가 결과를 보여주고 있다. 각 항목별 평가 점수를 더하여 하도의 안정성을 평가하였다.
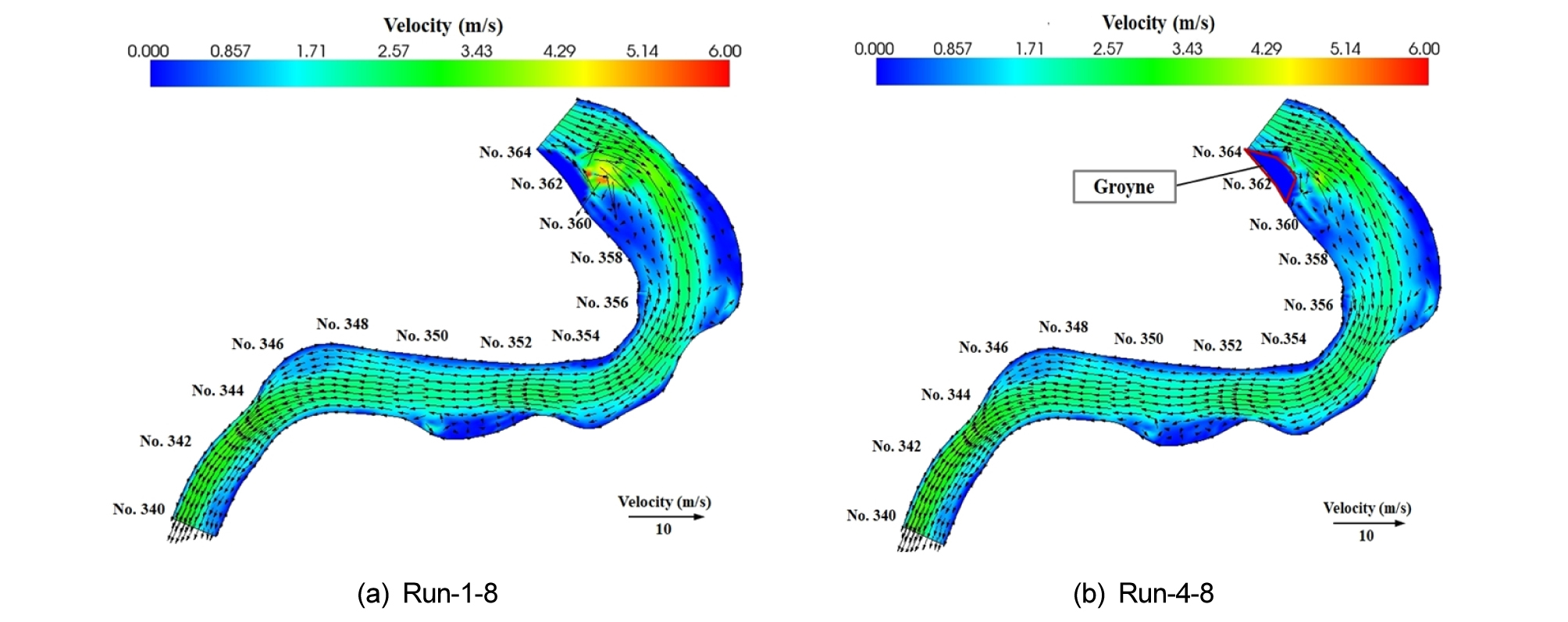
Fig. 11은 Runs 1-8과 4-8의 수치모의 결과를 보여주고 있다. 수제의 직하류에서는 수제를 통과하는 흐름이 역류하는 순환구역이 발생한다 (Fig. 11). 또한, 수제설치 구간에서는 통수단면이 감소하면서 평균유속과 단위 폭 당 유량을 증가하였다. 그러나 홍수 시에 유속은 Run-4-8 일 때 1.21 - 3.02 m/s로 수제 설치 전 Run-1-8의 1.32 - 3.12 m/s보다 0.1 m/s 정도로 작으며, 큰 차이가 없었다 (Fig. 12). 이러한 현상은 유량이 증가함에 따라 관성력이 지배적이고, 상대조고가 작아지므로, 수리구조물에 의한 2차류의 영향이 작기 때문으로 판단된다.
Table 6은 수치모의를 수행하여 결과에 대하여 Table 3에서 제시한 평가점수를 적용한 결과를 보여주고 있다. 저수로 안정성 평가는 주수로를 기준으로 좌안과 우안으로 나누어 평가를 하였다. 하폭 대 수심의 비, 사행도, 하상경사 항목에서의 평가값은 각각 4.79, 4.08, 2.0으로 수제의 개수에 따른 변화 없이 동일한 것으로 나타났다. 유속의 경우에는 수제의 설치 개수가 증가할수록 수제가 설치된 우안에서는 평가값이 3.167에서 3.065까지 점차 감소하였으며, 좌안에서는 3.224에서 3.132로 평가값이 감소하였다. Shields number는 수제의 설치 개수가 증가할수록 수제가 설치된 우안에서는 평가값이 2.768에서 2.742까지 점차 감소하였으며, 좌안에서는 2.843에서 2.794로 감소하였다 (Table 6).
수제가 설치된 우안에서는 수제의 설치 개수가 증가할수록 평가값은 3.361에서 3.335로 감소하였다. 수제가 설치되지 않은 좌안에서는 우안에 설치된 수제의 개수가 증가할수록 평가값은 3.387에서 3.359로 감소하는 것으로 나타났다. 따라서, 수제의 수가 증가할수록 하도의 안정성이 증가하는 것으로 나타났다.
Table 6. Evaluation scores for each zone of study reach
6. 결 론
본 연구에서는 2차원 수치모형을 적용하여 수제설치에 의한 흐름특성을 분석하고, 저수로의 안정성을 평가하였으며, 그 결과는 다음과 같다.
1) 저수로 안정성 평가지표를 개발하기 위한 평가 항목은 대상구간의 수리, 지형적 특성을 고려하여 하폭 대 수심의 비, 사행도, 하상경사, 하안 부근에서 유속, Shields number 등 5가지 항목으로 구성하였다. 또한 Likert 척도법을 이용하여 평가 항목을 5등급으로 구분하고, 등급별 평가값을 정량화하여 평가지표를 개발하였다.
2) 하폭 대 수심의 비, 사행도, 하상경사 항목에서의 평가값은 수제의 설치 개수에 따른 변화 없이 동일한 것으로 나타났다. 유속과 Shields Number 항목의 경우에는 수제의 설치 개수가 증가할수록 평가값이 감소하는 것으로 나타났다.
3) 좌안과 우안에 대한 하도 안정성 평가에 대한 종합값을 분석한 결과, 좌안과 수제가 설치된 우안 모두에서 수제의 설치 개수가 증가할수록 평가값이 감소하였다. 따라서, 동일한 유량 조건일 때 우안에서는 수제 설치 전ᐧ후에 대한 하도의 개선효과가 있는 것으로 나타났으며, 수제의 설치 개수가 증가할수록 하도의 안정성이 증가하는 것으로 나타났다.
본 연구에서 개발한 하도 안정성 평가지표는 하도에서 치수적으로 불안정한 구간을 판별하여 수제설치로 인한 치수대책의 검토 및 수립을 지원할 수 있을 것이다. 본 연구에서는 5가지 항목에 대해서만 하도의 안정성 평가를 수행하였지만, 향후 연구를 통해 다양한 평가항목을 추가하며, 더욱 정밀한 평가기준을 개발해야 할 것이다.