1. 서 론
2. 연구 방법
2.1 연구 지역
2.2 습지 생태네트워크 구성
2.3 네트워크 특성 분석
2.4 토지이용변화 시나리오
3. 결 과
3.1 분산모델 별 네트워크 특성
3.2 토지이용변화에 의한 생태 네트워크 기능의 변화
4. 고 찰
5. 결 론
1. 서 론
습지는 인류에게 다양하고 유용한 재화와 서비스를 제공해주는 생태계 요소로써 지속가능한 발전을 가능하게 하는 자연기반 해법기술의 주요대상으로 고려되고 있다 (Luo et al. 2011, Thorslund et al. 2017). 특히 거시적 규모에서 인류와 생태계 등 지구환경시스템의 지속가능한 발전을 위한 포괄적 개념으로의 자연기반 해법기술은 자연 생태계의 인위적 간섭을 줄이고 훼손된 생태계를 복원하는 새로운 프레임워크로 대두되고 있다 (Eggermont et al. 2015, Steffen et al. 2015). 하지만 과거 개별 습지의 기능회복, 생태계 서비스 분석 등 단일 습지에 대한 중점적 연구에 비해 거시적 관점에서의 습지 간 상호 연결성에 기반한 경관 규모의 연구는 미흡하며 (Zedler 2000, Cui et al. 2012), 이에 따라 습지경관 내에 공간적으로 분산되어 있는 습지를 대상으로 습지경관의 기능을 정량화하여 분석하기 위해 네트워크 관점의 연구가 필요하다 (Kim and Park 2019, 2020). 생태 네트워크 관점의 분석은 경관 내 습지 간 연결의 동역학적 복잡성 분석에 유용한 도구로써 생태 네트워크의 구성요소인 습지 간의 상호 작용을 통해 습지경관의 기능을 파악할 수 있다 (Fletcher et al. 2011, Phillips et al. 2015). 또한 네트워크 내에서의 개별 습지의 구조적, 기능적 특성을 파악하여 대상 습지의 보전가치를 평가할 수 있으며 개별 습지 변화 발생 시 거시적 관점에서 습지경관의 기능에 미치는 영향을 파악할 수 있다 (Rho 2013). 특히 습지와 습지 간 연결을 활용한 생태 네트워크 모델링 및 네트워크 토폴로지 분석을 통한 습지경관의 기능 파악은 거시적 습지 경관을 이루는 구성요소 간의 상호 연결성을 기반으로 외부교란에 대한 동역학적 현상 연구가 가능하며, 생태 네트워크 상에서의 서식지 이동경로 보존 및 허브에 대한 취약점 분석 등 회복탄력적 생태 네트워크를 위한 습지 보전 및 대체습지 설치와 같은 생태계 보전계획을 위한 다양한 자연기반의 공학적 해법 도출의 기반을 마련할 수 있다 (Pastor-Satorras and Vespignani 2001, Peterson 2002).
본 연구는 습지경관의 개발에 대응하기 위한 자연기반 해법기술로서의 공학적 해법을 도출하기 위해 각 네트워크 모델의 구조적, 기능적 특성 분석을 통해 습지경관의 기능을 평가하며, 택지개발 시나리오를 가정하여 생태 네트워크 내 다수 습지의 파괴에 따른 습지경관 기능의 변화를 분석하였다. 이를 위해 경관에 분포되어 있는 습지를 노드로 정의하고 가상 서식 종의 분산 모델에 따라 구성되는 이동 통로를 링크로 정의하여 생태 네트워크를 모사하였다.
2. 연구 방법
2.1 연구 지역
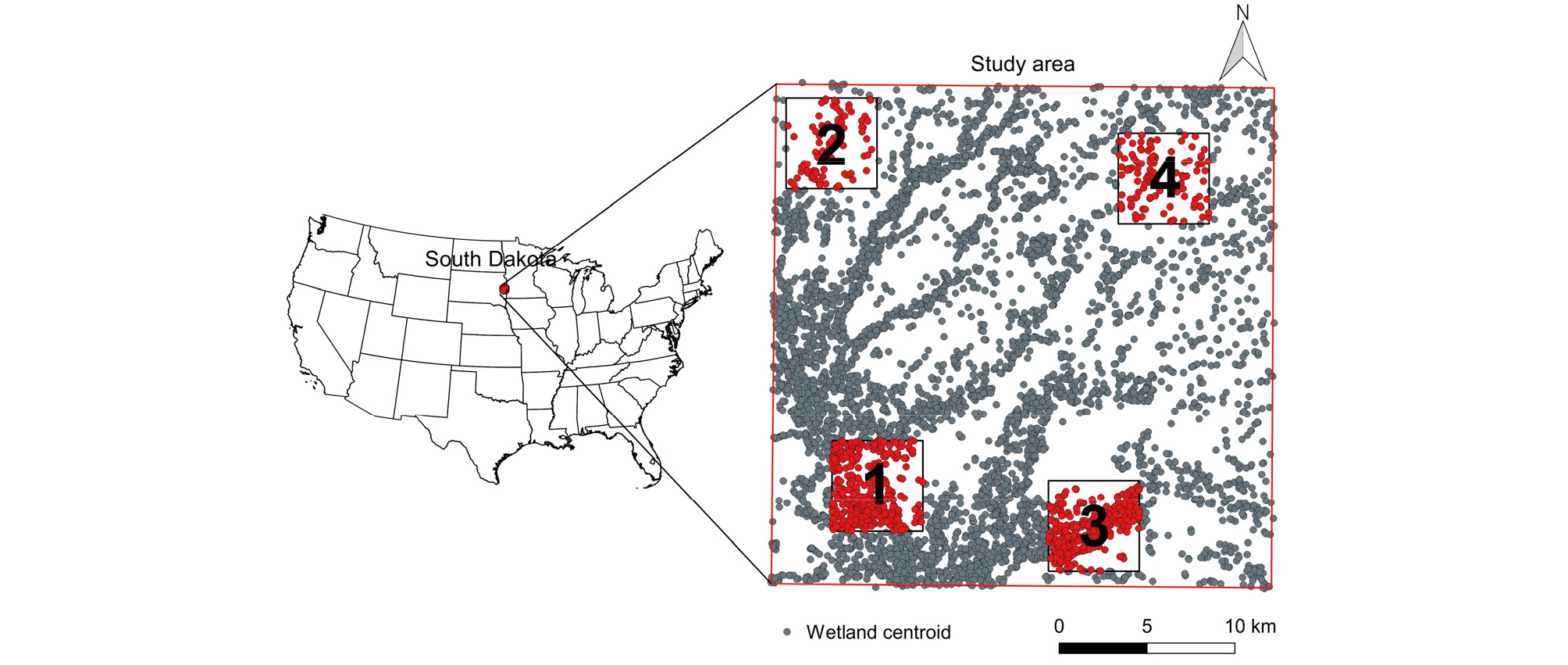
본 연구는 습지 기능의 중요성 및 보호계획의 필요성이 대두되었던 미국 South Dakota주에 위치한 Prairie pothole region (PPR)을 연구 대상지로 선정하였다 (Preisser et al. 2000). 해당 지역은 수많은 습지가 분포하는 습지경관을 이루고 있으며 연간 0.38% 정도의 습지 손실률을 보임에 따라 습지경관의 변화로 인한 영향 분석이 필요하다 (Johnston and McIntyre 2019). 이 지역에는 북미 철새 종의 약 50% 이상이 서식하는 등 다양한 생물종에 대한 서식지간 이동 모사의 타당성을 제공하며, 서식종의 이동을 기반으로 한 네트워크 구조화가 용이하다 (Kim and Park 2020). 특히 연구지역인 South Dakota는 2010년 기준 0.3%의 가장 낮은 도시비율 (Urban land/Total land)을 보이는 지역 중 하나이다 (주 (state) 기준 46위). 도시에 거주하는 인구비율 또한 56.7%로 주 기준 44위에 해당하나 꾸준한 성장세를 보여온 지역이며 (1970년: 44.6%; 1980년: 46.4%; 1990년: 50.0%; 2000년: 51.9%; 2010년: 56.7%), 낮은 도시화율로 인한 도시 인구밀도가 787명/km2으로 높게 나타나는 등 (주 기준 인구밀도 26위) 도시지역 개발에 대한 수요가 발생하는 지역이다 (US Census Bureau (https://data.census.gov/)). 또한 2006년부터 2012년의 기간 동안 경작지는 1,439,500 에이커 (5,825.4 km2) 증가하였고 도시지역 또한 27,400 에이커 (110.9 km2) 증가하는 등의 토지이용 변화가 지속되고 있다 (Reitsma et al. 2014).
본 연구에서는 Brookings County에 포함되는 Level IV Ecoregion, Big Sioux Basin (ID #: 46 m) 중 30.5 km × 30.5 km에 해당하는 구역을 공간적 범위로 설정하였으며 (Fig. 1), 지리적으로 고립된 습지 (Geographically Isolated Wetland, GIW) 5,534개를 대상으로 연구를 진행하였다. 습지 정보는 U.S. Fish & Wildlife Service에서 제공하는 NWI (National Wetlands Inventory (https://www.fws.gov/)) 데이터를 이용하였으며, QGIS 2.18.18을 활용하여 연구 데이터를 분류하였다.
2.2 습지 생태네트워크 구성
본 연구에서 활용하는 생태 네트워크는 서식 종의 분산에 따라 연결되는 습지로 구성되며 이러한 모델링을 통한 분석은 서식지 간의 생태학적 연결성을 분석하는데 주로 활용되어왔다 (Bunn et al. 2000, Amezaga et al. 2002, Uden et al. 2014). 본 연구에서는 다양한 서식종의 이동모델을 모사하고 차이점을 분석하기 위해 결정론적 분산 모델 (Model Ⅰ: 임계거리 분산모델 (threshold distance)) 과 확률론적 분산 모델 (Model Ⅱ: 지수분포 분산 모델 (exponential dispersal kernel); Model Ⅲ: Lévy flight에 기반한 두꺼운 꼬리 분산 모델 (heavy-tailed dispersal model))을 활용하여 네트워크를 구성하였다 (Kim and Park 2020). Model Ⅰ은 임계 거리에 포함되는 모든 습지를 연결하여 네트워크를 구성하는 간단한 모델링 방법으로 해석이 용이하여 기존 습지 네트워크 연구에 활발하게 이용되었으나 장거리 이동 분석이 불가능하다 (Minor and Urban 2008, Reynolds and Rhodes 2009, Wright 2010, McIntyre and Strauss 2013, O’Farrill et al. 2014). 본 연구에서는 양서류 분산 거리에 대한 기존 연구를 참고하여 90종의 최대 이동거리 중 최빈값인 1 km의 임계거리를 적용하였다 (Smith and Green 2005). 또한 지수분포 확률에 기반한 제한적 장거리 이동 모사가 가능한 Model Ⅱ (Eq. 1)와 멱함수 확률에 기반한 무제한적 장거리 이동 모사가 가능한 Model Ⅲ (Eq. 2)를 활용함으로써 장거리 이동에 의한 생태 네트워크를 구성하였다 (Urban and Keitt 2001, Kim and Park 2020).
| $$P\left(x\geq d_1\right)=e^{-\alpha x}$$ | (1) |
여기서 d1는 노드 사이의 거리, α-1는 종의 평균 분산 거리이며, 본 연구에서는 임계 거리 모델 (threshold distance model) 적용 시 형성되는 평균 분산 거리인 600 m를 평균 분산 거리로 적용하였다 (Kim and Park 2020). 또한 지수 함수로 표현이 불가능한 거리에 제한이 없는 장거리 이동을 표현하기 위해 Lévy flight model에 기반한 두꺼운 꼬리 분산 모델을 활용하였다 (Bartumeus 2007, Schick et al. 2008, Kim and Park 2020).
여기서 x는 노드 사이의 거리, β는 멱함수의 지수이며, α2는 정규화 인수로 α2=(β-1)xmin(β-1)이다. 또한 멱함수 적분을 위한 최소 임계거리 (xmin)는 100 m로 설정하였다. 본 연구에서는 이동 확률이 가장 낮게 나타나는 모델을 적용하였다 (Reynolds and Rhodes 2009). 또한 습지 모양을 실제 면적과 동일한 면적을 갖는 원형으로 가정하여 습지 간 최단 거리를 산정하여 노드 간의 거리를 계산하였다 (Kim and Park 2020).
2.3 네트워크 특성 분석
앞서 구성한 3가지 모델의 생태 네트워크의 특성을 분석하고, 노드 제거로 인한 영향을 파악하기 위해 평균 연결성 (mean degree, <k>), 네트워크 효율성 (efficiency, E) 및 집단화 계수 (clustering coefficient, cc)를 계산하였다 (Table 1). 노드의 연결성 (node degree)은 네트워크를 이루는 노드 중 핵심 노드를 판별하기 위한 가장 쉬운 방법으로 노드가 지니는 연결의 수로 정의된다 (Irwin and Hughes 1992, Jordán et al. 2008, Pereira et al. 2011). 효율성은 네트워크를 구성하는 전체 노드 사이의 효율적 이동을 측정할 수 있는 지표이며 집단화 계수는 노드에 연결되어 있는 서로 다른 노드들의 연결 정도를 측정하는 도구로 네트워크의 군집성을 판별할 수 있는 방법이다 (Watts and Strogatz 1998, Newman 2003, Boccaletti et al. 2006, Latora and Marchiori 2007).
Table 1.
Network metrics and their mathematical formula
| Network metrics | Mathematical formula |
| Degree (k) | , |
| Efficiency (E) | |
| Clustering coefficient (cc) |
2.4 토지이용변화 시나리오
본 연구에서는 습지 경관 내 5.5 km × 5.5 km규모의 4개 구역에 대한 토지이용변화를 가정하여 해당구역의 단독 또는 복수의 개발로 인한 습지의 제거가 습지경관 내에 구성된 생태 네트워크의 기능에 미치는 영향을 분석하여 개발로 인한 기능의 손실 산정기법을 마련하고자 하였다. 토지이용변화 면적은 미국 인구조사국 (US Census Bureau)에서 실시한 2010년 조사를 기반으로 연구 지역인 South Dakota 지역이 도시 인구 비율과 유사한 Arkansas 주 (1970년: 50.0%; 1980년: 51.6%; 1990년: 53.5%; 2000년: 52.5%; 2010년: 56.2%)에 조성된 계획도시 중 가장 최근인 1974년에 조성되고 인구밀도가 유사한 도시인 Maumelle를 기반으로 결정하였다 (면적: 31.26 km2; 인구밀도: 582명/km2).
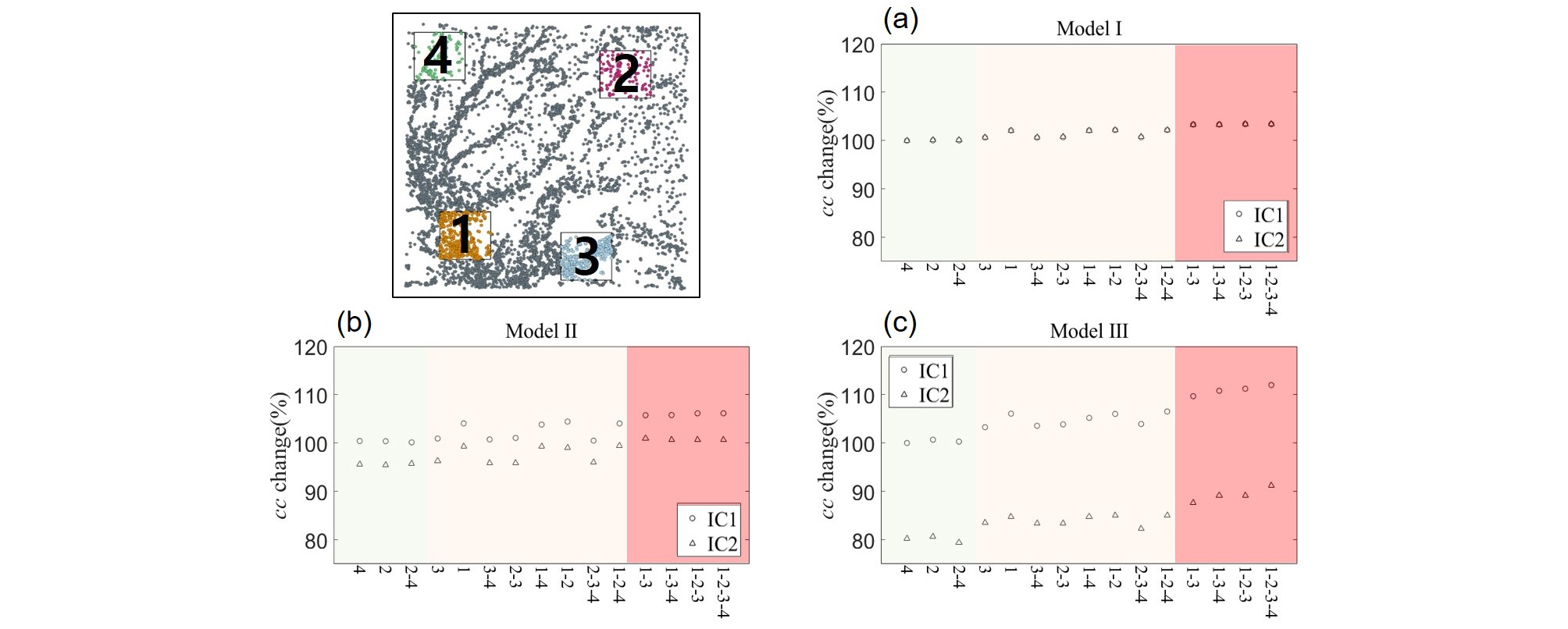
Fig. 1에서와 같이 1, 3 구역은 습지 밀도가 높은 개발구역으로 가정하였으며 (ρ1 = 11.97개/km2; ρ3 = 11.01개/km2) 2, 4 구역은 밀도가 낮은 개발구역으로 가정하였다 (ρ2 = 4.07개/km2; ρ4 = 3.17개/km2). 또한 습지 면적에 따른 네트워크 변화의 특성을 분석하기 위해 2가지의 초기 면적조건 (습지 면적의 합/최대 습지 면적의 합)을 대상으로 연구를 진행하였다 (IC1 = 1; IC2 = 0.59).
3. 결 과
3.1 분산모델 별 네트워크 특성
연구지역에 분포하고 있는 습지와 서식종의 세 가지 분산모델로 모사한 생태 네트워크의 구조적 차이점과 토지이용변화로 야기되는 습지경관 기능성의 변화를 파악하기 위해 초기 네트워크의 평균 연결성 (<k>), 네트워크 효율성 (E) 및 집단화 계수 (cc)를 분석하였다 (Table 2). 초기 네트워크는 각 습지의 최대면적 상태를 기반으로 구성하였다.
Table 2.
Initial network properties of the three dispersal models
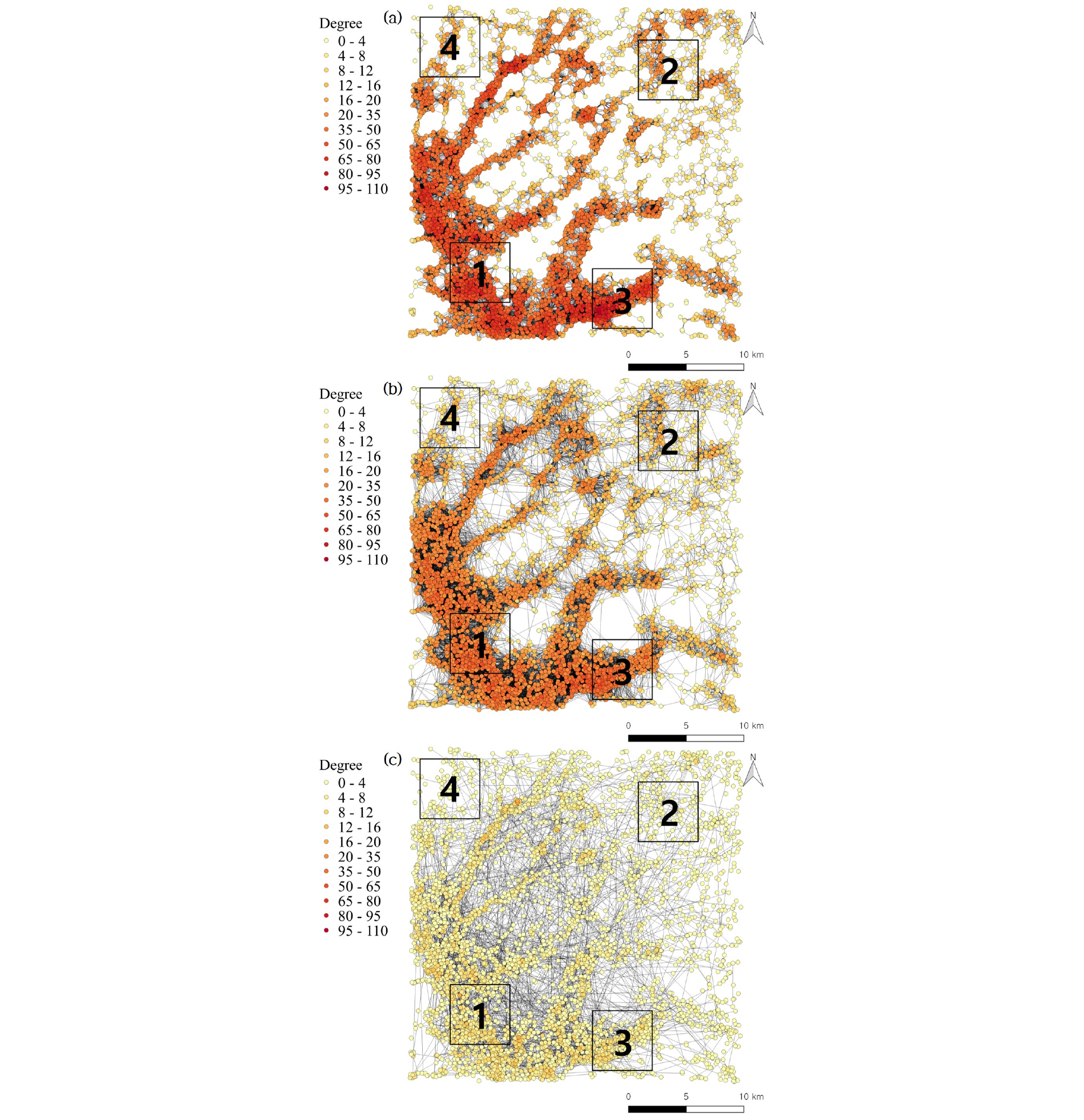
결정론적 분산모델인 Model Ⅰ은 확률론적 분산모델인 Model Ⅱ와 Ⅲ에 비해 평균 연결성 (<k>)과 집단화 계수 (cc)가 큰 것으로 나타났다. 특히 Model Ⅰ은 임계거리 내의 습지간 국지적 연결이 확률론적 분산모델에 비해 상대적으로 많이 형성됨에 따라 집단화 계수가 높게 나타난다 (Fig. 2 (a)). 반면 노드 간 이동거리가 짧음으로 인해 장거리 이동을 위해서는 다수의 노드를 거쳐야 하는 비효율적인 특성을 지닌다.
확률론적 분산모델 (Model Ⅱ, Ⅲ)의 경우 Model Ⅰ에 비해 국지적 연결이 적게 형성됨에 따라 <k>와 cc가 낮으나 장거리 이동이 가능함에 따라 (Fig. 2 (b) and 2 (c)) 네트워크를 구성하는 노드 간의 이동 효율성 (E)은 높게 나타난다.
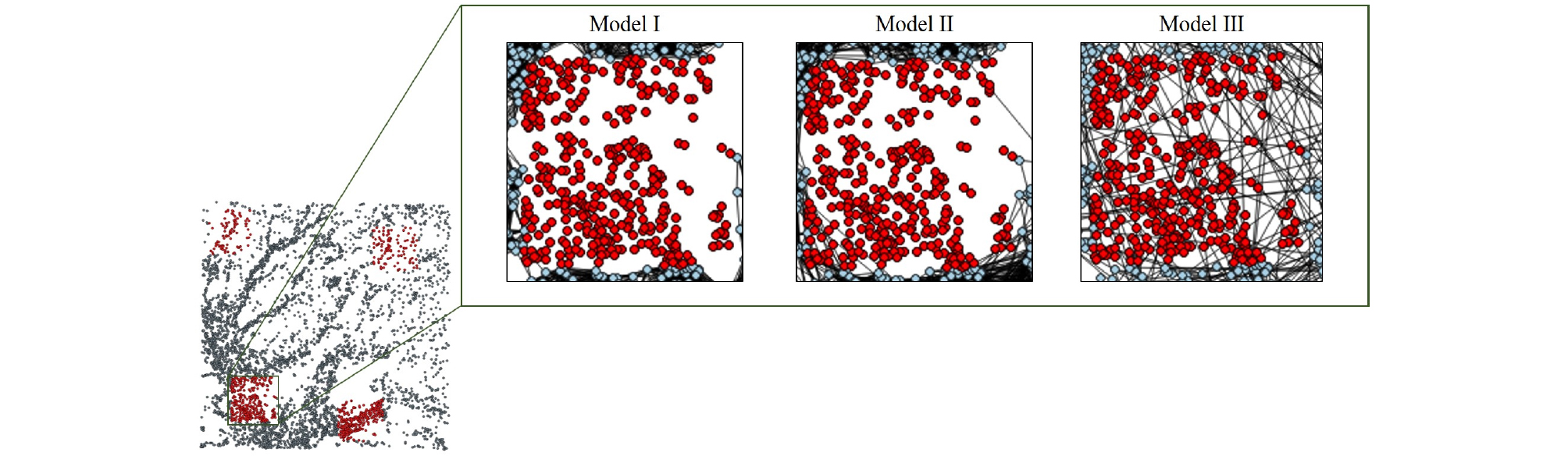
또한 각 분산 모델 별 생태 네트워크의 핵심 노드 (연결성이 높은 노드, 허브)의 일관성을 파악하기 위해 각 노드 별 연결성의 피어슨 상관계수를 분석한 결과 모든 네트워크 구조에서 상관계수가 높게 나타나는 것을 확인하였다 (Table 3). 즉, 결정론적 분산모델에서의 핵심 노드가 확률론적 분산모델에서도 핵심 노드 역할을 수행하는 것으로 나타났다. 특히 Fig. 2를 통해 어떠한 생태 이동 모형을 택하더라도 1, 3번 구역이 2, 4번 구역에 비해 허브가 많이 분포되어 있는 것을 볼 수 있다.
3.2 토지이용변화에 의한 생태 네트워크 기능의 변화
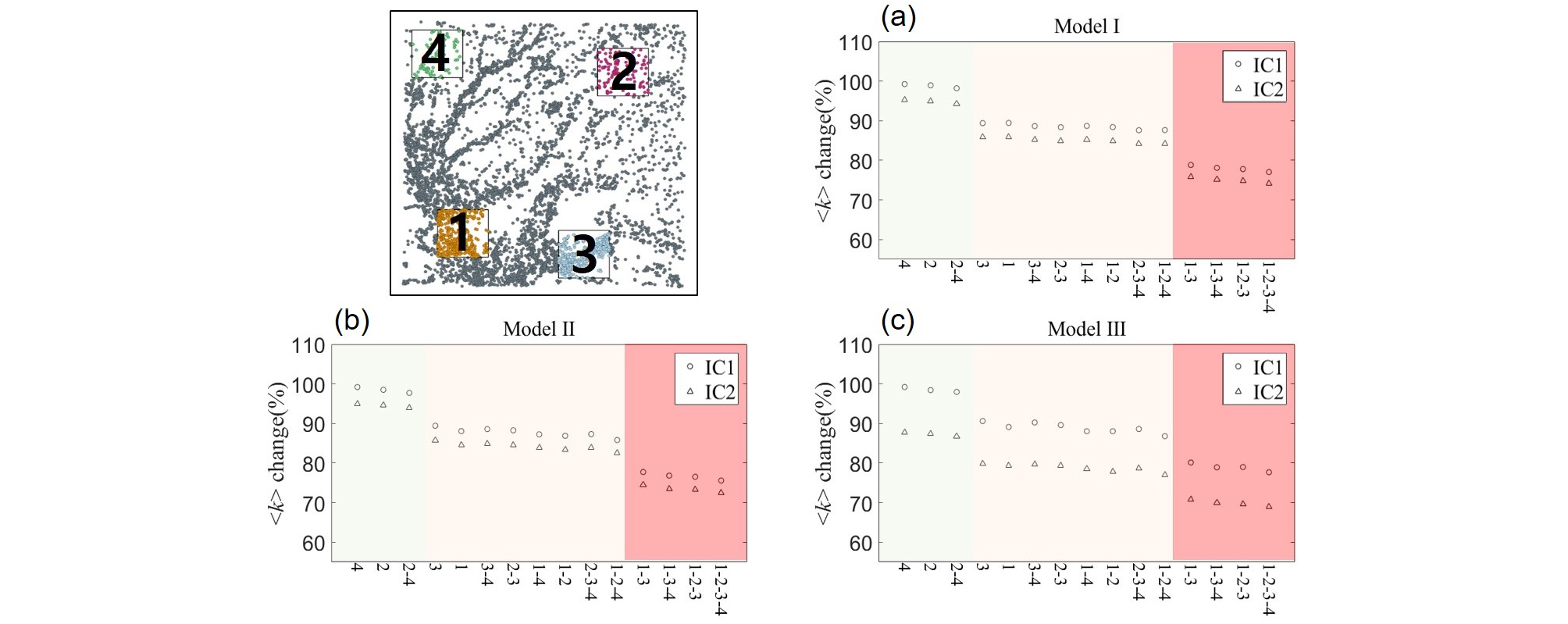
IC1의 모든 네트워크 모델에서 노드가 제거됨에 따라 평균 연결성 (<k>)이 감소하였으나 각 구역의 밀도 및 허브의 존재 유무에 따라 피해의 정도가 다른 것을 확인하였다. 밀도가 낮고 허브의 분포가 적은 구역이 제거된 경우 노드 제거에 따른 <k>의 감소가 적게 나타났으며 (Model Ⅰ (4 구역: 99.3%; 2 구역: 99.0%), Model Ⅱ (4 구역: 99.2%; 2 구역: 98.5%), Model Ⅲ (4 구역: 99.2%; 2 구역: 98.4%)) 해당 구역이 동시에 제거되는 경우에도 초기 값의 98.2% (Model Ⅰ), 97.7% (Model Ⅱ), 98.0% (Model Ⅲ)로 소폭 감소하였다. 반면 노드의 밀도가 높고 허브가 존재하는 1 구역과 3 구역의 노드가 제거된 경우 동일 면적이 제거되었음에도 기능의 감소폭이 증가하였으며 (Model Ⅰ (3 구역: 89.4%; 1 구역: 89.4%), Model Ⅱ (3 구역: 89.4%; 1 구역: 88.1%), Model Ⅲ (3 구역: 90.6%; 1 구역: 89.1%)) 밀도가 낮은 구역과 동시에 노드가 제거될 때 88.7 - 87.6% (Model Ⅰ), 88.6 - 85.8% (Model Ⅱ), 90.2 - 86.8% (Model Ⅲ)로 1, 3 구역만 제거되는 경우에 비해 소폭 감소하는 등 1 구역과 3 구역의 제거로 인한 영향이 큰 것을 확인할 수 있다. 특히 1 구역과 3 구역이 동시에 제거되는 경우 78.8% (Model Ⅰ), 77.7% (Model Ⅱ), 80.1% (Model Ⅲ)로 <k>가 크게 감소하였으며 모든 구역이 제거되었을 때 77.0% (Model Ⅰ), 75.6% (Model Ⅱ), 77.7% (Model Ⅲ)까지 감소하였다 (Fig. 3).
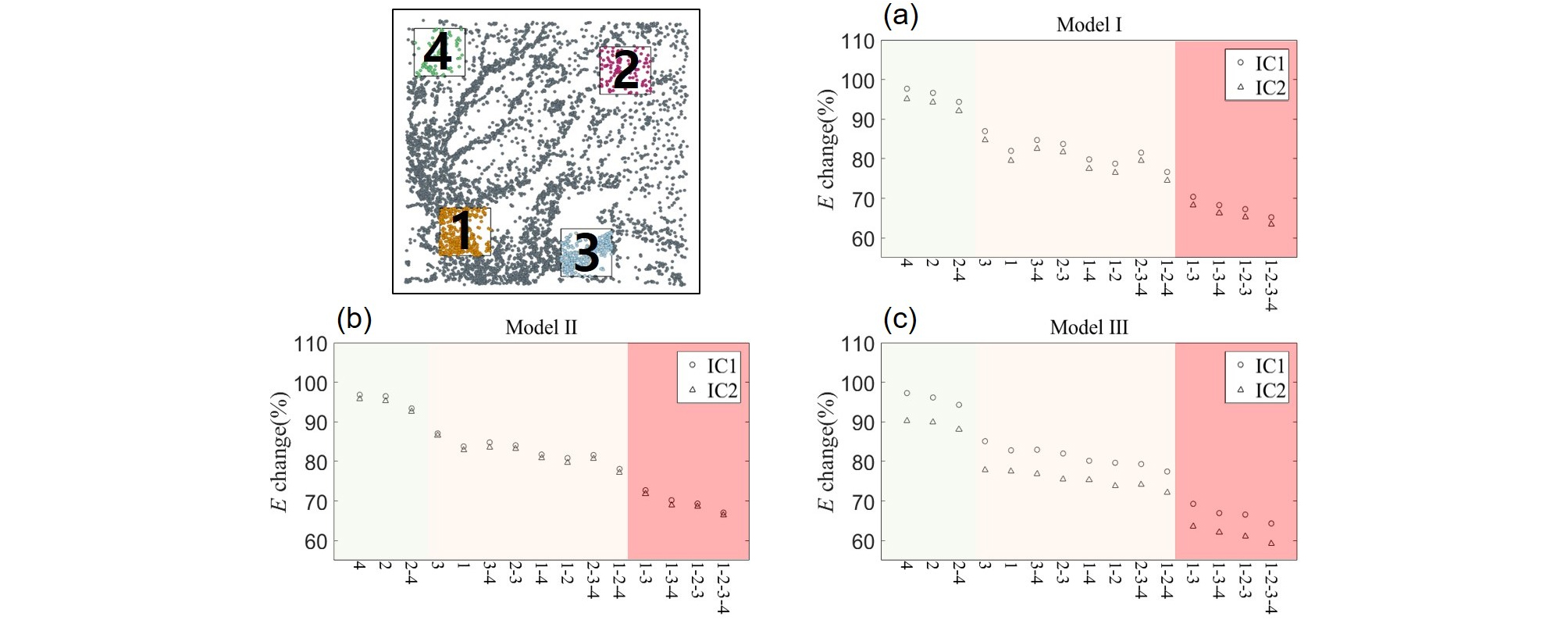
이동 효율성 (E) 또한 모든 네트워크 모델에서 노드가 제거된 경우 감소하였다. 밀도가 낮은 구역이 제거된 경우 소폭 감소하였으며 (Model Ⅰ (4 구역: 97.7%; 2 구역: 96.6%), Model Ⅱ (4 구역: 96.8%; 2 구역: 96.5%), Model Ⅲ (4 구역: 97.3%; 2 구역: 96.1%)) 동시에 제거되는 경우에도 초기 값의 94.4% (Model Ⅰ), 93.4% (Model Ⅱ), 94.3% (Model Ⅲ)로 감소하였다. 밀도가 높고 허브가 존재하는 구역이 제거된 경우 <k>와 유사하게 감소폭이 증가하였으며 (Model Ⅰ (3 구역: 87.0%; 1 구역: 82.0%), Model Ⅱ (3 구역: 87.1%; 1 구역: 83.8%), Model Ⅲ (3 구역: 85.1%; 1 구역: 82.8%)) 특히 1, 3 구역이 동시에 제거되는 경우 70.4% (Model Ⅰ), 72.7% (Model Ⅱ), 69.3% (Model Ⅲ)로 크게 감소하는 등 밀도가 높고 허브가 존재하는 구역의 노드가 제거되었을 때의 영향이 큰 것을 확인하였다. 특히 E의 경우 모든 구역에 대한 제거에 대해 <k>의 변화보다 큰 폭의 감소를 보였다 (Fig. 4).
집단화 계수 (cc)의 변화는 <k>와 E의 변화와는 달리 노드가 제거된 경우 증가하는 현상을 보인다. 밀도가 낮은 2, 4 구역이 제거된 경우 초기 값과 유사하거나 소폭 상승하며 (Model Ⅰ (4 구역: 100.0%; 2 구역: 100.0%), Model Ⅱ (4 구역: 100.4%; 2 구역: 100.4%), Model Ⅲ (4 구역: 100.0%; 2구역: 100.7%)) 밀도가 높은 1, 3 구역이 제거된 경우 또한 노드가 제거됨에 따라 cc는 상승하였다 (Model Ⅰ (3 구역: 100.6%; 1 구역: 102.1%), Model Ⅱ (3 구역: 100.9%; 1 구역: 104.1%), Model Ⅲ (3구역: 103.3%; 1 구역: 106.1%)). 특히 1, 3 구역의 노드가 동시에 제거되는 경우 103.3% (Model Ⅰ), 105.8% (Model Ⅱ), 109.7% (Model Ⅲ)로 상대적으로 상승폭이 증가하였으며 모든 구역의 노드가 삭제되면 103.4% (Model Ⅰ), 106.2% (Model Ⅱ), 112.0% (Model Ⅲ)로 상승하는 등 연결이 감소함에 따라 습지의 군집화는 증가하는 것을 확인하였다 (Fig. 5). IC2의 경우 면적의 감소로 인한 노드 간 거리의 증가로 네트워크 특성이 감소하였으나 각 구역 내 노드 제거에 의한 영향은 IC1과 유사하다.
4. 고 찰
본 연구에서는 토지이용의 변화 및 개발 등에 의한 습지경관에 대한 피해를 최소화하기 위한 자연기반해법 도출을 위한 사전 단계로써 습지경관 내 습지와 서식종의 이동경로로 모사되는 생태 네트워크를 기반으로 가상의 토지개발 시나리오로 인한 습지경관 기능의 변화를 분석하여 토지개발에 의한 피해를 산정하였다.
토지이용변화에 의한 생태 네트워크의 변화를 분석한 결과, Model Ⅰ에서 밀도가 높은 지역 중 3 구역 (ρ = 11.01개/km2)을 제거한 경우 평균 연결성 (<k>) 초기 값의 89.40%의 평균 연결성을 유지하며 1 구역 (ρ = 11.97개/km2)을 제거한 경우 89.44%를 유지하는 것으로 나타났다. 즉, 밀도가 더 높은 구역을 제거했음에도 불구하고 기능의 감소는 상대적으로 적었다. 이는 3 구역을 제거한 경우 1 구역을 제거했을 때 보다 더 많은 습지 간의 연결이 제거되어 발생한 결과로 파악되었다 (1 구역: 10,321 개; 3 구역: 10,359 개). 이를 통해 3 구역에 허브 역할의 노드가 많이 분포되어 있음을 유추할 수 있다. 반면, 확률론적 분산모델 (Model Ⅱ, Ⅲ)에 기반한 네트워크의 경우 밀도가 더 높은 1 구역을 제거했을 때 피해가 더 큰 것으로 나타났으며 이는 1 구역에서 제거되는 연결의 수가 많은 것이 원인임을 확인하였다 (Model Ⅱ (1 구역: 7,537 개; 3 구역: 6,633개), Model Ⅲ (1 구역: 1,383 개; 3 구역: 1,170 개). 이를 통해 분산모델에 따른 생태 네트워크의 연결 중심성이 높은 허브의 위치는 유사하나 (Table 3) 분산모델에 따른 차이는 존재하며, 습지경관의 토지개발 시 허브의 위치와 토지개발 구역 내 노드의 수 등 다양한 변수를 통합적으로 분석해야 할 필요성을 유추할 수 있다.
이동 효율성 (E)의 분석 결과 <k>의 변화와 유사하게 밀도가 높은 구역의 노드를 제거했을 때의 영향이 큰 것으로 나타났으나 <k>의 감소폭이 99.3 - 77.0% (Model Ⅰ), 99.2 - 75.6% (Model Ⅱ), 99.2 - 77.7% (Model Ⅲ)인 반면 E의 감소폭은 97.7 - 65.2% (Model Ⅰ), 96.8 - 67.1% (Model Ⅱ), 97.3 - 64.3% (Model Ⅲ)로 서식종의 습지경관 내 거시적 이동에 악영향을 끼치는 것을 확인하였다. 즉, 개발구역 내의 허브 (연결성이 높은 노드)가 네트워크 내의 효율적인 장거리 이동을 가능하게 하는 징검다리 (stepping-stone)역할을 하는 매개 중심성 (BC: betweenness centrality)이 높은 노드의 역할을 함께 수행한다는 것을 유추할 수 있다. 특히 Fig. 6에서와 같이 Model Ⅲ의 경우 개발구역 내 노드가 제거됨에도 해당 구역을 건너뛸 수 있는 장거리 이동이 가능하나 노드 제거로 인한 E가 가장 크게 감소하였다. 이는 Model Ⅲ에서의 허브가 매개 중심성 또한 가장 높은 노드의 역할을 하는 것으로 판단된다.
집단화 계수 (cc)는 노드 제거로 인한 거동이 <k>와 E와는 달리 증가하는 것으로 나타났다. 이는 개발구역 내의 노드와 외부의 노드 간 연결이 제거됨으로 인해 군집성이 더욱 높아진 것으로 판단된다. Model Ⅰ의 경우 네트워크 전체의 <k>와 cc는 35.3과 0.38이나 밀도가 높은 1 구역과 3 구역의 <k>와 cc는 41.3, 0.38 (1 구역)과 53.1, 0.41 (3 구역)으로 유사하거나 높은 값을 지닌다. 반면 각 구역과 외부 노드와는 평균 7.86개 (1 구역), 4.55개 (3 구역)의 상대적으로 매우 낮은 연결을 지닌다. 즉, 노드가 제거되기 전 군집화를 이루지 못한 연결이 존재하였으나 개발지역의 노드가 제거됨에 따라 군집화가 증가한 것으로 판단된다. Model Ⅱ와 Ⅲ 또한 개발지역 내 노드와 외부 노드와의 적은 수의 연결이 파괴됨에 따라 군집성이 증가하는 것으로 판단된다 (Model Ⅱ (1 구역: 7.95개; 3 구역: 4.65개), Model Ⅲ (1 구역: 1.23개; 3 구역: 0.80개)). 본 연구를 통해 거시적 습지경관의 토지이용 변화에 대응하기 위한 공학적 솔루션 도출 방법으로써의 습지경관 구성요소 기반 생태 네트워크 모델링 및 분석방법을 검토하였다. 생태 네트워크 모델링은 습지경관 구성요소의 구조적, 기능적 핵심습지의 공간적 분포파악이 용이하며 특히 노드의 파괴에 의한 기능의 감소를 발생시키는 요인에 대한 미시적 분석이 가능한 것을 확인하였다. 이를 기반으로 습지의 동역학적 거동에 의한 습지경관의 기능을 유지 또는 향상시킬 수 있는 공학적 솔루션 도출의 방법론으로 활용할 수 있을 것으로 판단된다.
5. 결 론
본 연구에서는 습지경관 내 토지이용변화로 인한 영향을 최소화하기 위한 자연기반해법 도출의 기반을 마련하기 위해 생태 네트워크를 정의한 후 다양한 토지개발 시나리오를 적용하여 생태 네트워크 기능의 변화를 분석하였다. 또한 다양한 서식종의 분산능력 모사를 위해 임계거리를 활용한 결정론적 분산모델과 두 개의 확률론적 분산모델을 적용하여 생태 네트워크를 구성하였다. 결정론적 분산모델에서 군집화가 높게 나타나고 장거리에 대한 이동 효율성은 낮게 나타나는 반면 확률론적 분산모델에서는 군집화는 낮으나 장거리 이동의 효율이 상대적으로 높게 나타나는 구조적 차이점이 관찰되었으나 (Kim and Park 2020) 토지개발 시나리오에 의한 노드 제거에 대해 밀도가 높고 허브가 존재하는 구역의 노드를 제거할 경우 평균 연결성과 이동 효율성이 크게 감소하며 군집화는 증가하는 결과가 공통적으로 관찰되었다.
본 연구 결과는 향후 습지경관 내의 개발 시 경관 내 서식종의 서식지 이동에 대한 영향을 판단할 수 있는 기초자료로 활용될 수 있다. 특히 구조적, 기능적 핵심 역할을 하는 노드를 판별할 수 있으며 이를 통해 토지개발 후보지역에 대한 우선순위 판단에 근거자료를 제시할 수 있을 것으로 사료된다. 또한 본 연구를 통해 마련한 연구방법은 불가피한 토지개발에 대해 대체 습지 설치로 인한 영향 분석이 가능하여 대체 습지 조성을 위한 후보지 선정에 용이할 것으로 판단된다.