1. 서 론
2. 실험장치 및 내용
2.1 실험장치
2.2 실험 내용
3. 차원해석
4. 결과 및 분석
4.1 수리특성 분석
4.2 다중회귀분석
4.3 회귀모형식의 유의성 검정
4.4 독립변수들의 다중공선성 검토
5. 결 론
1. 서 론
하천과 수로에서의 연직수문은 수위조절, 조수의 역류방지, 각종 용수의 취수 기능을 가지는 대표적인 하천시설물이다. 일반적으로 하천에 설치되는 고정보나 연직수문은 보 상류로부터 유입된 유사가 보 하류로 배출되지 못하고, 퇴적이 발생하여 그에 따른 저류량 감소, 홍수위 상승, 수질악화 등의 문제가 발생한다. 이러한 문제를 해결하기 위해 하단배출형 연직수문의 도입이 요구되며, 연직수문의 퇴적토 배출 특성뿐만이 아닌 퇴적토를 수반한 유출에 따른 수리특성 분석이 필요하다.
수문의 수리특성에 관한 연구로는 Rajartnam and Subramanya (1967)는 수문의 유량계수는 구조물 상하류 수심차와 관련이 있는 것을 확인하였다. Yen et al. (2001)은 실험을 통해 게이트 하류의 수축부와 보 상하류 수심의 함수로 자유월류와 잠수월류를 구분하여 수리특성을 분석하였다. Razi et al. (2008)은 수문 주변의 수면형상 분석을 통해 유량, 수심과 수문의 개도높이가 수문 하류부의 수면형상에 지배적임을 확인하였다. Cassan and Belaud (2011)는 연직수문에서 정확한 유량산정을 위해 보 상하류에서의 흐름특성을 수치모형과 수리모형을 통해 분석하였다. Oskuyi and Salmasi (2012)는 연직 연직수문에서 자유월류와 잠수월류의 경계에 따른 선형과 비선형 형태의 유량계수 결정식을 제시하였다. Shayan et al. (2014)은 sluice gate와 radial gate 설치에 따른 에너지-운동량 방정식을 이용한 수축계수의 변화와 자유월류, 잠수월류에 따른 수문에 작용하는 힘을 분석하였으며, radial gate 형태와 개도높이에 따른 수축계수의 특성을 규명하여 유량계수 산정을 위한 수축계수를 제시하였다. Choi et al. (2016)은 수리모형을 통해 다단식 하단배출형 연직수문의 하류부 흐름을 자유월류와 잠수월류로 구분하여 수리특성 분석과 유량계수 관계식을 제시하였다.
Bakhmeteff and Matzke (1979)는 실내실험을 통해 수력도약의 길이가 Froude 수가 증가함에 따라 함께 증가하는 것을 확인하였다. Hayawi and Mohammed (2011)는 수문 하류의 수력도약과 에너지 손실의 특성을 연구하여 수력도약에 따른 에너지 소산은 Froude 수와 Weber 수의 관계로 제시하였다. Jung (2011)은 보 설치에 따른 세굴심과 세굴길이 산정을 위한 이동상 수리실험을 실시하여 하상보호공 길이 산정공식을 제시하였으며, 기존의 하상보호공 산정공식과의 비교를 수행하였다. 수문 상하류 수심차와 개도높이 비에 따른 상하류 유속비와 Froude 수 변화에 따른 수력도약 효율변화에 대한 관계식을 제시하였다. Park et al. (2013)은 보의 효과적인 설계 및 운영방법을 위해 월류형 보와 하단 방류형 보의 흐름 특성, 하류부 수의 변화에 따른 수력도약 길이의 분석과 보 형태에 따라 단위거리당 발생되는 비에너지 손실량을 비교분석하였다.
이와 같은 수문의 수리특성에 관한 연구는 수문 상류에 퇴적된 퇴적토를 배제한 상태에서의 수리특성 연구가 주를 이루었으며, 퇴적토의 이동을 수반한 수리특성 연구는 부족한 실정이다.
본 연구에서는 퇴적토의 이동을 수반한 하단배출 형태의 연직수문을 대상으로 유량계수와 수력도약의 수리특성을 분석하기 위해 수리 모형실험을 수행하였다. 유량계수와 수력도약특성을 지배하는 무차원 매개변수를 도출하기 위해 차원해석을 실시하였다. 1차 실험은 퇴적토를 배제한 상태에서 연직수문의 개방도와 유량을 조절하여 수리실험을 수행하였고, 2차 실험에서는 수문 상류에 퇴적토를 포설하여 퇴적토의 높이, 유량과 수문 개방도에 따른 수리실험을 수행하였다. 수리실험을 통해 퇴적토가 없을 경우와 퇴적토를 포설한 경우의 수리특성과 Froude 수와의 관계를 분석하고 퇴적토를 고려한 유량계수, 수력도약 높이, 수력도약 길이의 관계식을 제시하였다. 아울러 개발된 회귀식의 적용성을 검토하기 위하여 개발된 식에 의한 예측값과 실측값 간의 예측구간의 정확도를 제시하고 아울러 통계적인 특성을 제시하였다.
2. 실험장치 및 내용
2.1 실험장치
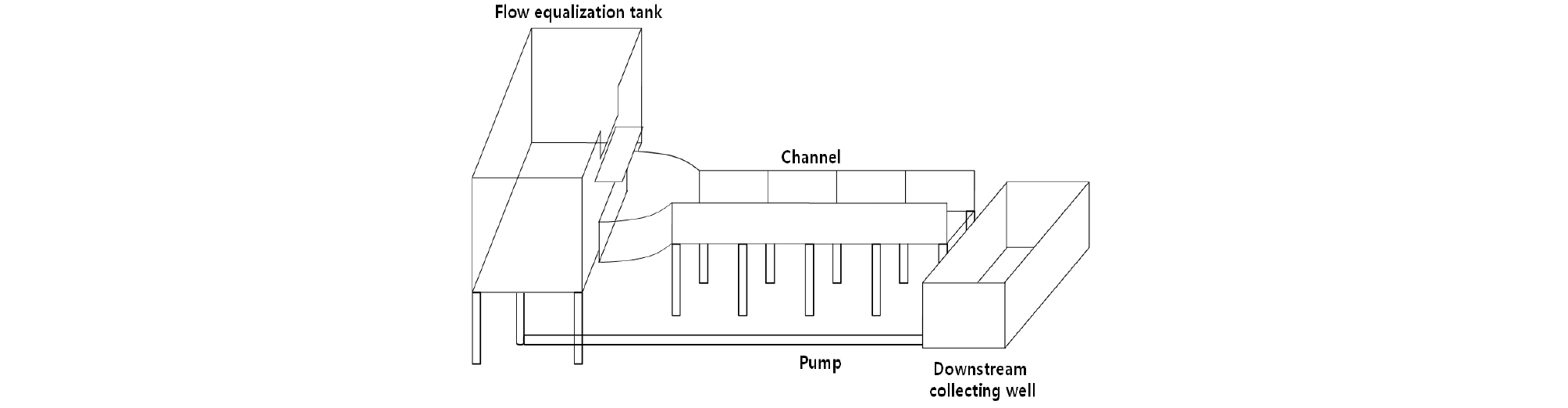
하단배출형 연직수문에서의 퇴적토 배출을 수반한 수리특성의 분석을 위한 실험은 Fig. 1에서와 같이 개도높이 (openness height)의 조절이 가능한 연직수문을 대상으로 실시하였다. 연직수문은 4 mm의 steel 재질로 제작하였으며, 하단부는 예연위어 형식으로 처리하여 위어에 따른 흐름마찰을 감소시켰다. 실험장치는 수로와 유량공급부로 저류조, 펌프가 있으며 실험수로는 유량조절조, 모형수로, 하류 집수정으로 구성되었다. 모형수로는 폭 0.4 m, 깊이 0.4 m, 길이 10 m의 직사각형 수로로 유량공급능력은 최대 0.05 m3/s이다 (Fig. 2).
2.2 실험 내용
실험은 수문 상류의 퇴적토 유무에 따른 수문 주변의 흐름특성을 확인하기 위해 수문 개방도, 유량조건과 퇴적토 높이를 달리하여 수행하였다. 유량은 유량공급배관의 밸브 조절은 통해 0.013 m3/s, 0.014 m3/s, 0.016 m3/s의 3가지 유량, 퇴적토 높이는 퇴적토가 없는 경우와 퇴적토의 높이가 0.030 m, 0.040 m, 0.050 m의 3가지, 수문의 개방도는 0.030 m, 0.040 m, 0.050 m의 3가지에 대해서 실험을 실시하였다 (Table 1). 포설에 사용된 퇴적토는 4 mm의 자갈입경을 사용하였다.
Table 1. Experimental conditions
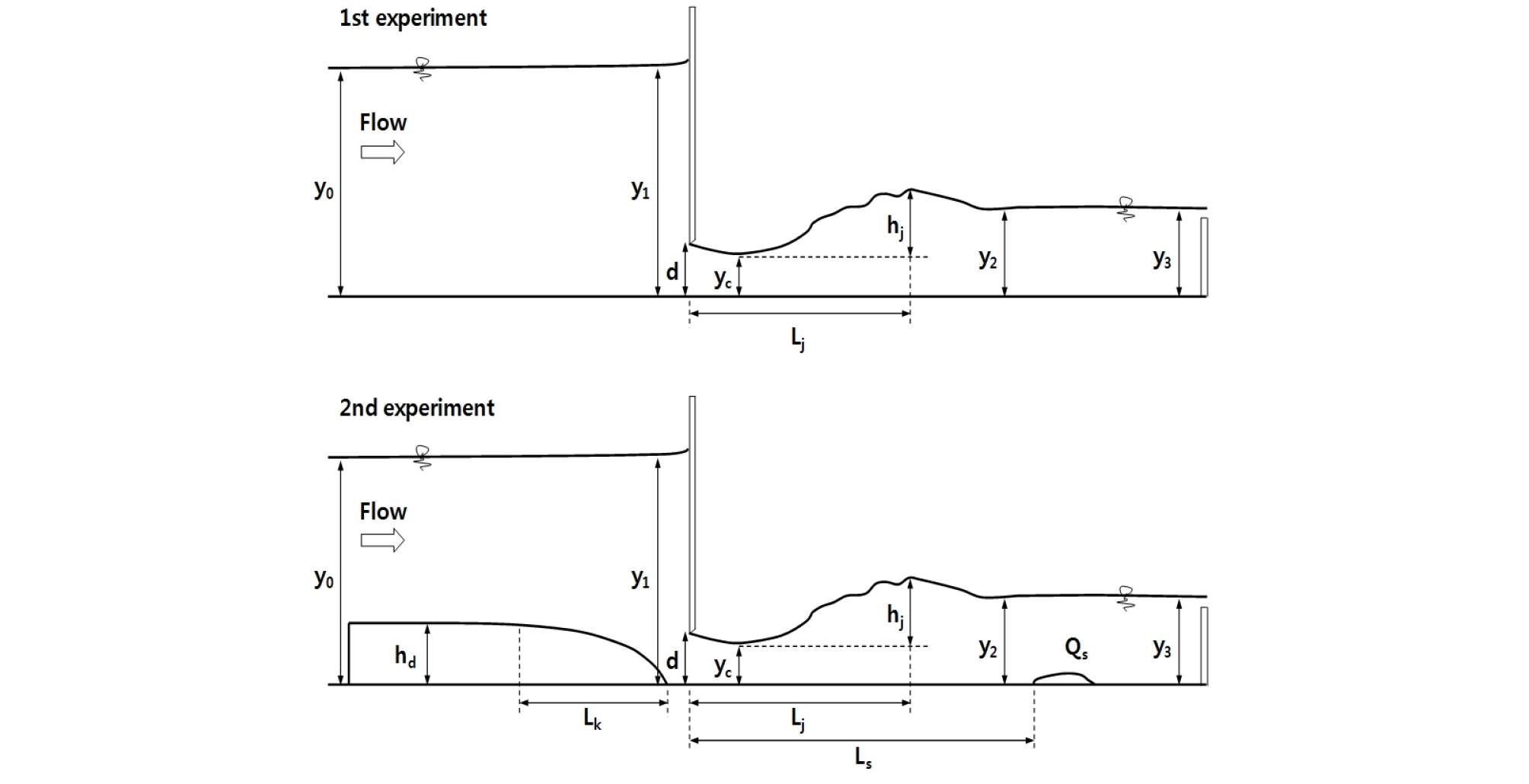
유량과 퇴적토 높이 변화에 따라 수심측정은 Fig. 3의 측정지점으로 포인트 게이지를 사용하여 수로 중심선에서 측정을 실시하였다. 수심측정을 위해 사용된 포인트 게이지의 측정범위는 0-410 mm로 측정단위는 1.0 mm이다.
안정된 수심을 유지하기 위해 충분한 통수시간 유지 후, 수심이 안정되었다고 판단된 시점에 수심을 측정하였다. Fig. 3의 y0는 유량이 유입되는 수로 시작점의 수심 (m), y1은 수문 직전의 상류수심 (m), yc는 수문 직하류 수축부 수심 (m), y2는 수력도약발생 후 안정된 수심 (m), y3는 하류단 수심 (m), d는 개방도 (m), hj는 수력도약 높이 (m), 수력도약 길이 (m), hd는 퇴적토 높이 (m), Lk는 보 상류 퇴적토의 두부침식거리 (m), Ls는 퇴적토 배출거리 (m), Qs는 퇴적토 이동량 (kg)이다.
3. 차원해석
수리실험을 통해 수문 주변 수리특성에 영향을 미치는 주요 인자들을 도출하였다. 도출된 인자들로 구성된 무차원 변수를 산정하기 위해 Buckingham의 π정리에 의하여 차원해석을 실시하였다.
수리특성에 영향을 미치는 주요 인자로 수문 직상류에서의 수심 (y1, m), 수축부 수심 (yc, m), 상하류 수심차 (y1-yc, m), 하류단 수심 (y3, m), 개방도 (d, m), 퇴적토 높이 (hd, m), 유량 (Q, m3/s), 유속 (V, m/s), 유체의 밀도 (ρ, kg/m3)와 수문 하류로 배출된 퇴적토의 배출거리 (Ls, m), 이동량 (Qs, kg)으로 변수들을 선정하여 이들 물리량 사이의 관계를 나타내는 방정식은 다음과 같다.
| $$f_1\left(y_1,\;y_c,\;y_1\;-y_c,\;y_3,\;d,\;h_d,\;Q,\;V,\;\mathrm\rho,\;L_s,\;Q_s,\;{C_d}_\;\right)=0$$ | (Eq. 1) |
| $$f_2\left(y_1,\;y_c,\;y_1\;-y_c,\;y_3,\;d,\;h_d,\;Q,\;V,\;\mathrm\rho,\;L_s,\;Q_s,\;{L_j}_\;\right)=0$$ | (Eq. 2) |
| $$f_3\left(y_1,\;y_c,\;y_1\;-y_c,\;y_3,\;d,\;h_d,\;Q,\;V,\;\mathrm\rho,\;L_s,\;Q_s,\;{h_j}_\;\right)=0$$ | (Eq. 3) |
여기서 f는 함수기호이며, Cd는 유량계수, Lj는 수력도약 길이 (m), hj는 수력도약 높이 (m)이다.
Eq. 1 - 3에서 차원해석을 위한 변수로 상류수심 (y1), 수축부 수심 (yc), 상하류 수심차 (y1-yc), 개방도 (d), 퇴적토 높이 (hd), 유량 (Q)을 선정하고, 질량차원, 길이차원과 시간차원을 각각 포함하는 하류단 수심 (y3), 유속 (V)과 유체의 밀도 (ρ)를 반복변수로 선정하여, 최종적으로 무차원 해석의 결과는 Eq. 4 - 6과 같다.
Eq. 4는 유량계수의 무차원 변수에 대한 식으로 하류단의 수심에 대한 수문 직상류 수심비 (y1/y3), 수축단면 수심비 (yc/y3), 수문 상류와 수축부 수심차의 비 ((y1-yc)/y3), 개방구간비 (d/y3), 퇴적토 높이비 (hd/y3), 유량과 수심간의 비 ((Q/(y32)×V)이고 퇴적토 수반에 따른 유량계수의 변화를 반영한 퇴적토 이동거리비 (Ls/y3)와 퇴적토 이동량비 (Qs/(y33ρ))이다. Eq. 5는 수력도약 길이비, Eq. 6은 수력도약 높이비의 무차원 변수에 대한 식으로 유량계수식과 동일하다.
| $$\varnothing_1(\frac{y_1}{y_3},\;\frac{y_c}{y_3},\;\frac{y_1-y_c}{y_3},\;\frac d{y_3},\;\frac{h_d}{y_3},\;\frac Q{y_3^{2\times V}},\;\frac{L_s}{y_3},\;\frac{Q_s}{y_3^3\rho},\;C_d)=0$$ | (Eq. 4) |
4. 결과 및 분석
4.1 수리특성 분석
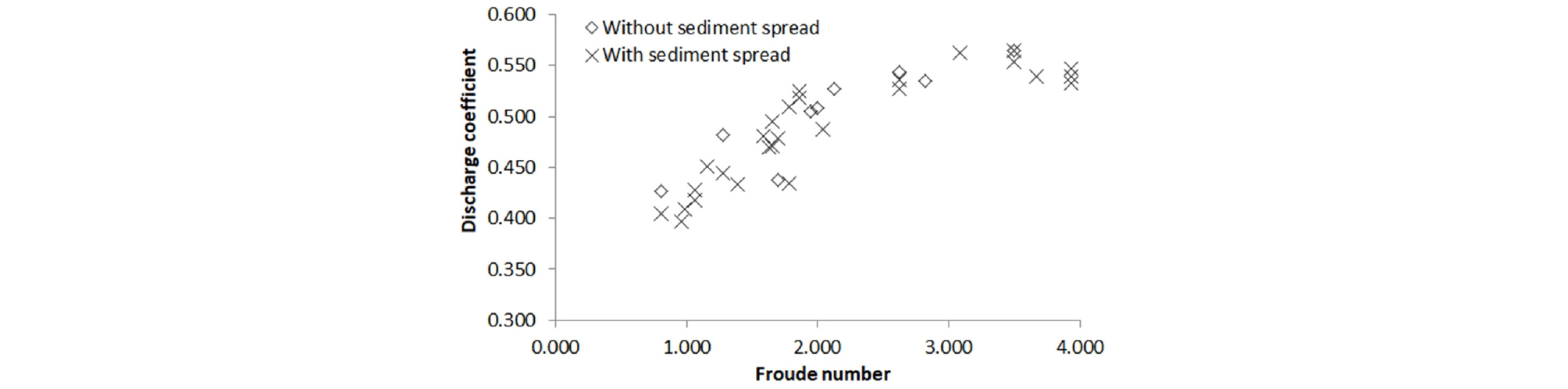
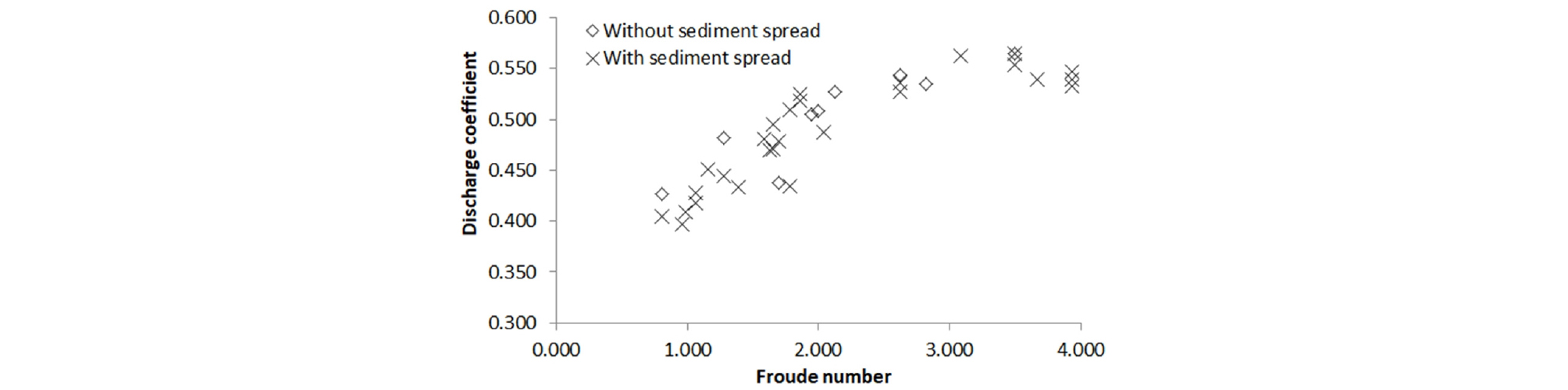
Fig. 4는 퇴적토의 포설 전과 후의 Froude 수에 따른 유량계수를 나타낸다. 퇴적토 포설 전의 유량계수의 범위는 0.43에서 0.56으로 지수함수적인 증가를 나타내고 있다. 반면에 포설 후의 유량계수는 0.40에서 0.56으로 퇴적토 포설이 없을 경우보다 감소하는 것으로 나타났다. 이는 수문 상류에 퇴적된 토사가 하류로 이동에 따른 수문의 개방구간에서의 토사의 이동과 흐름의 복합 상호작용으로 유량배제 능력을 저하시키는 것으로 판단된다. 따라서 토사의 이동을 수반한 유량계수 산정에는 토사의 이동특성을 나타낼 수 있는 변수를 도입한 유량계수 산정 방법이 필요한 것으로 판단된다.
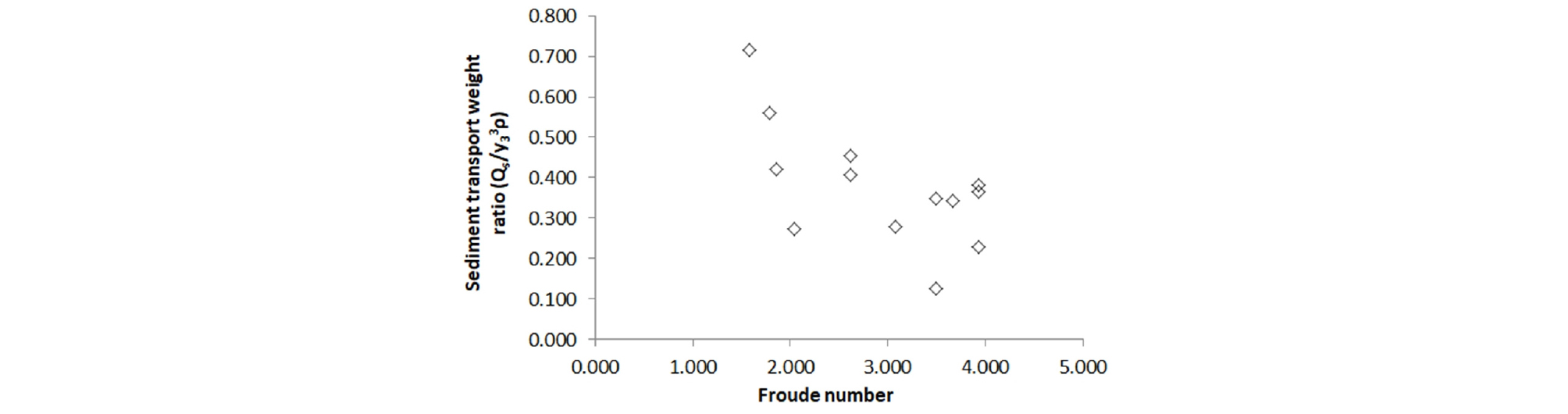
퇴적토를 수반한 흐름 시 유량계수는 Froude 수가 증가함에 따라 유량계수는 증가하는 양상을 보이며 Froude 수 3.0을 기점으로 감소하는 양상을 보인다. 이러한 현상은 연직수문에서 Froude 수가 크게 발달되는 경우는 작은 개방도에서 발생하는 조건이다. 개방구간이 작아짐에 따라 퇴적토의 이동이 상대적으로 흐름의 저항을 크게 나타나 통수능력을 저하시키는 현상으로 판단된다. 이는 Fig. 5의 Froude 수에 따른 퇴적토 이동량비에서와 같이 개방구간이 큰 Froude 수에서 퇴적토 이동량이 크게 나타나고 Froude 수 3.0까지 감소하다 초과하는 구간에서 강한 흐름으로 퇴적토 이동량이 증가되는 현상으로 설명이 가능하다.
Froude 수에 따른 수력도약의 특성을 분석하기 위해 Froude 수에 따른 수력도약 높이비와 수력도약 길이비를 비교하였다. Froude 수가 클수록 수력도약 전후의 수심비가 크게 되어 완전 수력도약이 되고, Frc=1-1.7사이에 있어서는 한계류보다 약간 큰 흐름으로 완전 수력도약이 되지 않고 파상 수력도약이 나타남을 확인하였다.
퇴적토 포설 전의 Froude 수의 범위는 1.9-3.5, 퇴적토 포설 후의 Froude 수는 1.6-3.9의 범위로 나타났다. 퇴적토 포설 전후 대부분의 경우에서 완전 수력도약으로 나타났으며, 퇴적토가 포설되었을 때 한가지 경우에서 파상 수력도약으로 나타났다.
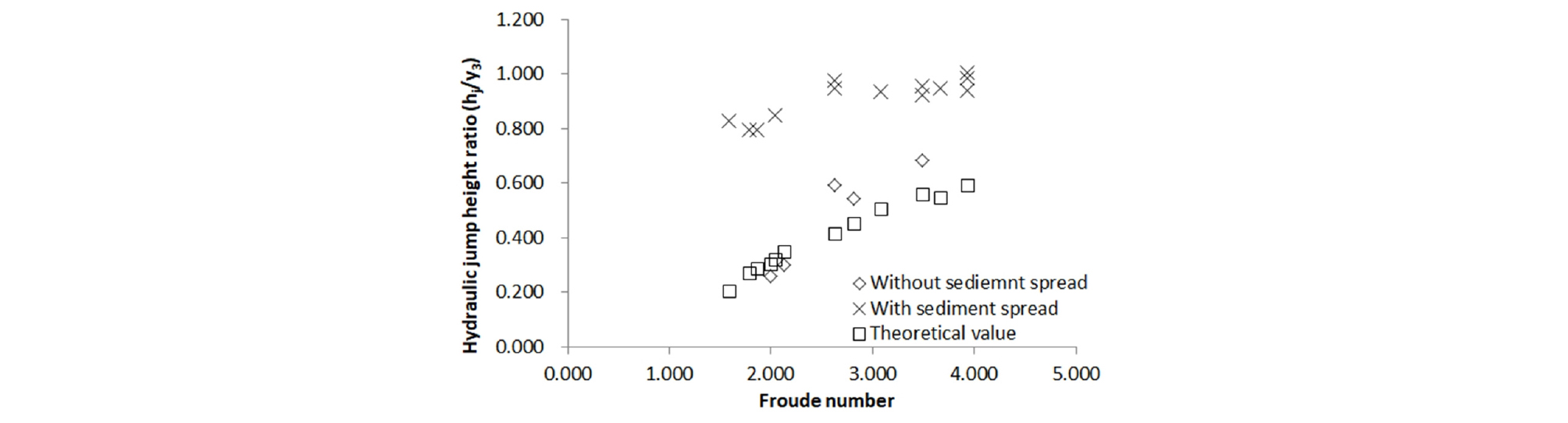
Fig. 6은 퇴적토 포설 전과 후의 Froude 수에 따른 수력도약 높이비 (hj/y3)이다. 퇴적토 포설 전과 후에 관계없이 Froude 수가 증가함에 따라 수력도약높이비가 증가하는 양상을 보였다. 퇴적토 포설 전의 수력도약 높이비는 0.26에서 0.68이고, 포설 후의 수력도약 높이비는 0.80에서 1.00이다. 수력도약 높이비는 퇴적토가 포설되어 있을 경우가 퇴적토가 없는 경우보다 큰 값을 보였다.
퇴적토가 있을 경우 Froude 수와 수력도약 높이비의 증가 양상이 완만하게 나타났고, 퇴적토가 없는 경우 보다 전반적으로 크게 나타났다. 이는 Fig. 5에서 Froude 수가 작더라도 하류부로 이동한 퇴적토의 증가에 따른 하류부 수심의 영향으로 수력도약 높이가 증가된 것으로 판단된다. 따라서 토사의 이동을 수반한 수력도약 높이의 산정에는 토사의 이동특성을 나타낼 수 있는 변수를 도입이 필요한 것으로 판단된다.
Eq. 7에 의한 수력도약 높이의 이론값과 실험에 의한 수력도약 높이의 관계를 비교하였다. 실험에 의한 수력도약 높이는 0.065 - 0.120 m이고, 이론식에 의한 수력도약 높이는 0.071 - 0.103 m로 작은 Froude 수에서는 유사하게 나타났으나, 큰 값의 Froude 수의 범위에서는 작게 나타났다.
| $$H_j=\frac{y_c}2(-1+\sqrt{1+8Fr_c^2})$$ | (Eq. 7) |
여기서 Hj는 수력도약 높이, yc는 수축부 수심 (m), Frc는 수축부에서의 Froude 수이다.
Fig. 7은 퇴적토 포설 전과 후의 Froude 수에 따른 수력도약 길이비 (Lj/y3)이다. 퇴적토 포설 전의 수력도약 길이비는 2.22에서 11.27이고, 포설 후의 수력도약 길이비는 1.41에서 11.27이다. 수력도약 길이비는 Froude 수의 관계는 Froude 수 3.0 이하에서는 유사하게 증가하는 양상을 보였으나, Froude 수 3.0 이상에서는 퇴적토가 포설되어 있는 경우 수력도약 길이비가 감소하는 것으로 나타났다. 이는 Fig. 5의 Froude 수에 따른 퇴적토 이동량비에서와 같게 수문 하류로 배출된 퇴적토의 영향으로 수력도약 길이에 영향을 미치는 것으로 판단된다.
4.2 다중회귀분석
수리실험결과를 이용한 유량계수, 수력도약 높이와 길이에 대한 회귀식의 유의성 검정을 실시하였다. 통계분석을 위해 사용된 프로그램은 IBM SPSS 22v.으로 데이터 관리 및 통계분석을 목적으로 개발된 소프트웨어로 교차분석, 상관분석, 회귀분석, 분산분석 등 복잡한 다변량 분석이 가능하다. 무차원 매개변수을 이용해 선정된 독립변수와 유량계수, 수력도약 높이와 길이의 종속변수에 대수를 취하여 선형형태의 관계식으로 변환하여 각각 회귀분석을 수행하였다.
회귀분석에서 무차원 매개변수인 독립변수의 선정은 후진 제거방법을 이용하였다. 후진 제거방법은 모든 독립변수를 포함하는 회귀모형을 만든 후 기여도가 가장 적은 변수부터 차례로 제거시켜 나가는 방법이다. 이에 따라 수리특성을 예측하기 위해 도출된 회귀식은 Eq. 8 - 13과 같다.
유량계수 회귀식이 수문 직상류의 수심비 (y1/y3)와 퇴적토 높이비 (hd/y3)의 함수로 결정될 경우 Eq. 8과 같다. Froude 수가 3.0을 초과 시 퇴적토 배출특성에 의해 유량계수 값이 감소하는 양상을 감안할 경우의 유량계수 회귀식은 수문 직상류 수심비, 퇴적토 높이비와 퇴적토 이동량비 (Qs/(y33ρ))의 함수인 Eq. 9가 적절하다. Eq. 8은 수문 상류에 퇴적토가 있을 경우 퇴적토 높이를 입력 변수로 사용하며, 퇴적토가 없을 경우는 퇴적토 높이비를 1의 값으로 입력하여 사용이 가능하다. Eq. 9도 동일하게 사용되며 수문 하류로 배출된 퇴적토가 있을 경우 퇴적토 이동거리비와 이동량비를 입력 변수로 사용하며, 퇴적토 이동량이 없을 경우 해당값을 1의 값으로 입력하여 사용이 가능하다.
| $$C_d=e^{-0.766}\times(\frac{y_1}{y_3})\times0.365\times(\frac{h_d}{y_3})\times0.031$$ | (Eq. 8) |
| $$C_d=e^{-0.743}\times(\frac{y_1}{y_3})\times0.270\times(\frac{h_d}{y_3})\times0.095\times(\frac{Q_s}{y_3^3\rho})-0.102$$ | (Eq. 9) |
수력도약 높이의 회귀식이 수문 직상류의 수심비와 퇴적토 높이비의 함수로 결정될 경우 Eq. 10과 같으며, 배출된 토적토의 영향을 고려한 수력도약의 높이의 회귀식은 상류 수심비, 퇴적토 높이비와 퇴적토 이동량비의 함수인 Eq. 11과 같다.
수력도약 길이의 회귀식이 수문 개방비와 퇴적토 높이비의 함수로 결정될 경우 Eq. 12와 같다. Froude 수가 3.0을 초과 시 퇴적토 배출특성에 의해 수력도약의 길이가 감소하는 양상을 감안할 경우 수력도약의 길이는 수문 개방비, 퇴적토 높이비와 퇴적토 이동량비의 함수인 Eq. 13과 같다. Eq. 10-13은 퇴적토가 없을 경우 퇴적토 관련 값은 1의 값을 이용하며, 퇴적토가 있을 경우 측정값을 이용하여 각각의 수리특성을 산정한다.
| $$h_j=y_3(e^{(-1.078)})\times(\frac{y_1}{y_3})\times0.902\times(\frac{hd}{y_3})\times(-0.464)$$ | (Eq. 10) |
| $$\begin{array}{l}L_j=y_3\left\{(e^{(-5.758)})\times(\frac d{y_3})\times(-5.358)\times(\frac{hd}{y_3})\times(0.264)\right\}\\\\\end{array}$$ | (Eq. 12) |
유량계수, 수력도약 높이와 수력도약 길이는 퇴적토 포설 전과 후의 데이터를 모두 사용하여 퇴적토를 고려한 회귀식을 도출하였다. 이렇게 도출된 회귀식은 퇴적토의 유무에 따라 사용될 수 있으며, 퇴적토 배출 현상을 고려한 Eq. 9, 11, 13에 대해서 유효성, 유의성 검정 및 다중공선성 검토를 수행하였다.
회귀식의 유효성을 판단하기 위한 지표로서 결정계수가 있다. Eq. 14에서와 같이 결정계수는 R2으로 표기하며 1에 가까울수록 우수한 회귀식임을 의미하나, 독립변수의 수가 증가될수록 값이 커지는 경향이 있어, Eq. 15의 수정된 R2값을 활용하여 회귀식의 유효성을 판단한다. 도출된 회귀식의 수정된 R2는 유량계수 0.749, 수력도약 높이 0.896, 수력도약 길이는 0.955로 나타났다.
| $$R^2=\frac{SSR}{TSS}=1-\frac{SSE}{TSS}$$ | (Eq. 14) |
| $$\mathrm{Adjusted}\;R^{2\;}=1-\frac{n-1}{n-p-1}(1-R^2)$$ | (Eq. 15) |
여기서 TSS는 총 제곱합, SSR은 회귀 제곱합, SSE는 오차 제곱합, n은 표본의 개수, p는 설명변수의 개수이다.
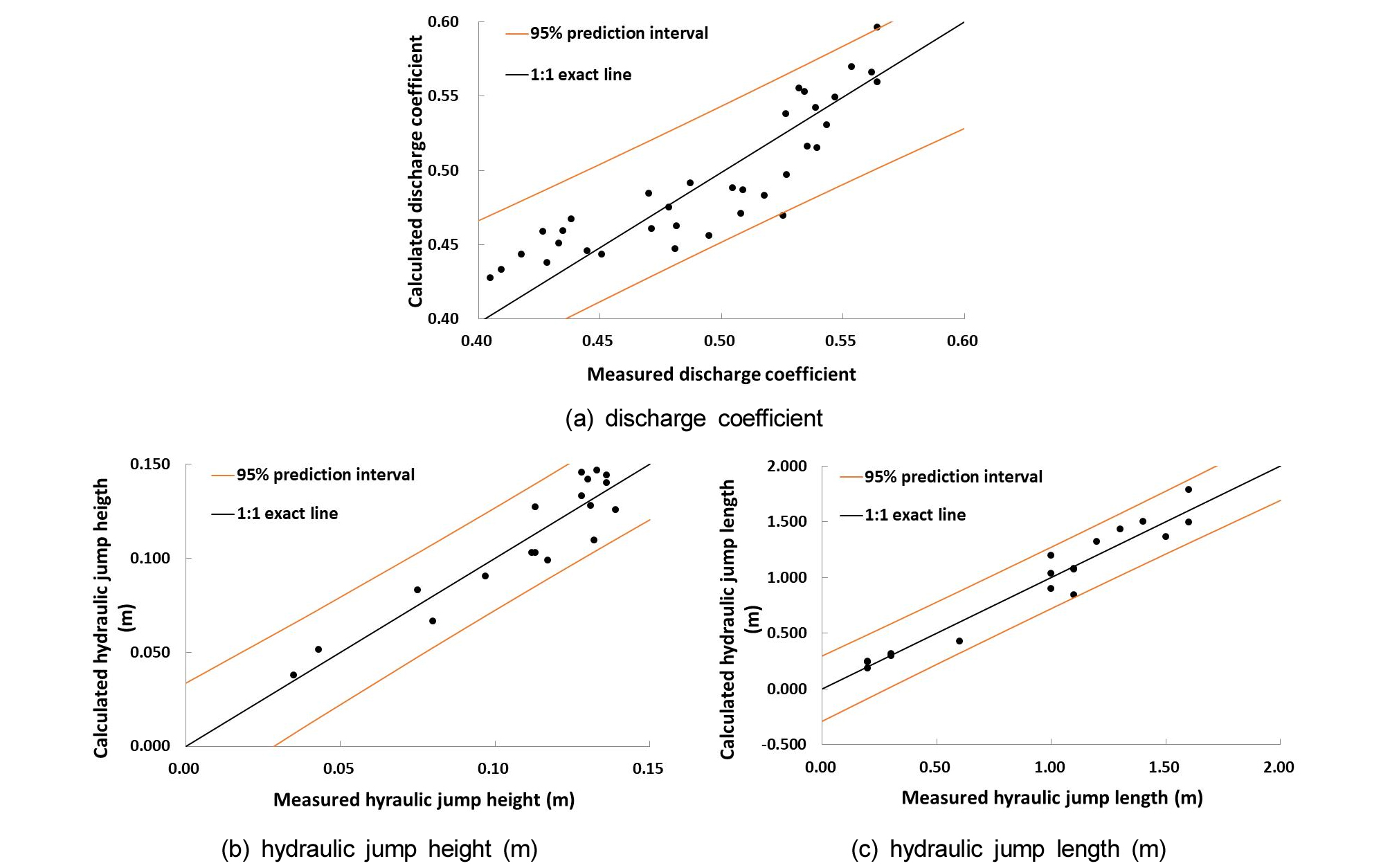
개발된 회귀식에 의한 각각의 수리특성의 예측값과 실제 측정값을 비교하여 개발된 식의 사용성을 평가하였다. Fig. 8에서 실선구간은 모형 예측값에 대한 95% 예측신뢰구간을 나타낸다.
유량계수의 회귀식의 예측값에 대한 95% 예측 신뢰구간에는 약 94%가 포함되었다. 수력도약 높이와 길이의 회귀식의 예측값에 대한 95% 예측 신뢰구간에는 100% 모두 포함되었다.
회귀분석의 기본 가정 사항 중 잔차의 독립성은 잔차가 다른 잔차에 영향을 미치게 되는 경우를 자기 상관이라고 하는데 자기 상관이 높으면 분석의 신뢰성을 잃게 된다. 잔차의 독립성은 Eq. 16의 Durbin-Watson 값으로 판단하게 되는데 0에 가까울수록 양의 자기상관, 4에 가까울수록 음의 자기상관이 있다고 판단하며, 2에 가까울수록 자기 상관이 없다고 판단한다. Durbin- Watson 값은 1.003에서 1.891으로 나타나 자기 상관이 없는 것으로 판단된다.
모의 값의 적절성을 나타내는 지표로 Nash-Sutcliffe Efficiency (NSE)가 있으며, NSE는 관측치와 모델의 관계를 이용하여 모델의 효율성을 평가하는 기법으로 모의 결과가 우수할수록 1에 가까운 값을 나타내며, Eq. 17에 의해서 계산된다 (Nash and Sutcliffe, 1970). 유량계수, 수력도약 높이와 길이에 대한 NSE값은 각각 0.774, 0.853, 0.984으로 모의 값이 적절함을 확인할 수 있다.
| $$\mathrm d=\frac{\sum_{t=2}^n(e_t-e_{t-1})}{\sum_{t=1^{e_t^2}}^n}$$ | (Eq. 16) |
| $$NSE=1-\left[\frac{\sum_{i=1}^n(O_i-P_i^2)}{\sum_{t=1}^n(O_i-\overline Q)^2}\right]$$ | (Eq. 17) |
여기서 O는 관측 값, P는 예측 값, 는 관측 값의 평균값, et는 시간 t에서의 오차이다.
또한 예측모델의 정밀도를 보다 객관적으로 평가하기 위해 실제 측정값과 예측한 값의 차이를 다룰 때 흔히 사용되는 RMSE (root mean square error)와 MAPE (mean absolute percentage error)를 도출하였다. 유량계수, 수력도약 높이와 길이에 대한 RMSE는 각각 0.034, 0.012 m, 0.120 m이고, MAPE는 각각 8.000%, 10.090%, 11.270%으로 나타났다 (Table 2).
Table 2. Multiple regression analysis results
Table 3. Results in the analysis of variance
4.3 회귀모형식의 유의성 검정
수리특성의 다중회귀분석을 통해 도출된 회귀모형의 유의성을 분산분석을 활용하여 검정한 결과, Table 4과 같은 결과를 도출하였다. 자유도 (df, degree of freedom)는 알 수 없는 모집단 모수의 값을 추정하고 이러한 추정치의 변동성을 계산하는데 “사용”할 수 있는 데이터가 제공하는 정보의 양으로, 표본의 관측치 수와 모형의 모수 수에 따라 결정된다. F값은 독립변수가 종속변수 예측에 도움이 되는지 판단하는 값으로, 유량계수, 수력도약 높이와 길이에 대한 도출된 회귀식의 F값은 각각 40.250, 50.077, 121.698로 나타났고 이에 대응하는 유의확률 (significance probability)이 모두 0.000으로 유의수준 0.05보다 작으므로 독립변수들 중 적어도 하나 이상의 변수는 종속변수를 설명하는데 유의하게 기여함을 나타낸다.
Table 4. VIF values for determining the multicollinearity of the independent variable
4.4 독립변수들의 다중공선성 검토
회귀식이 도출된 후에는 회귀모델의 유의성을 검정하고 다중공선성 (multi-co-linearity)을 분산팽창인자 (variance inflation factor, VIF)를 사용하여 확인하였다. 변수들 간의 다중공선성이 존재하는 경우, 다른 독립변수들의 결합으로 영향을 받는 독립변수가 회귀모형 내에서 독자적인 정보를 제공하지 못하게 되므로 R2의 값은 큰 반면에 대부분의 회귀계수들이 유의하지 않은 경우가 발생하게 된다. 다중공선성은 독립변수들 사이의 선형종속 (linear dependency)의 관계로 정의되며, 실질적으로 어느 독립변수가 다른 독립변수들로부터 밀접한 상관관계를 가지고 있는 상태를 말한다. 따라서 VIF의 유무를 확인하는 것이 바람직하며, VIF값이 10 이상이면 다중공선성이 존재한다고 판단하여 독립변수로 사용하지 않는다 (Ham, 2007).
사용된 독립변수의 VIF값은 Eq. 18에 의해 계산되었으며, VIF값은 Table 4에 나타내었다. 유량계수, 수력도약 높이와 길이에 대한 도출된 회귀식의 VIF값은 모두 10 미만으로 다중공선성은 없는 것으로 판단된다.
| $$\mathrm{VIF}=\frac1{1-R^2}$$ | (Eq. 18) |
5. 결 론
기존 연직수문의 수리특성에 관한 연구는 수문 상류에 퇴적된 토사의 이동이 없는 상태에서의 수리특성 연구를 수행하였다. 본 연구에서는 연직수문의 개방과 수문 상류의 퇴적토의 이동을 수반한 연직수문에서의 수리특성인 유량계수, 수력도약 높이와 길이에 대한 Froude 수와의 관계를 분석하고, 차원해석을 실시하여 수리특성에 영향을 미치는 무차원 매개변수를 도출하고, 이의 수리특성의 회귀식을 제시하고 적용성을 평가하였다.
1)유량계수가 포설 후의 유량계수보다 크게 나타났다. 이는 수문 상류에 퇴적된 토사가 하류로 이동에 따른 수문의 개방구간에서의 토사의 이동과 흐름의 복합 상호작용으로 유량배제 능력을 저하시키는 것으로 판단된다. 따라서 토사의 이동을 수반한 유량계수 산정에는 토사의 이동특성을 나타낼 수 있는 변수를 도입한 유량계수 산정 방법이 필요한 것으로 판단된다.
2)퇴적토 유무에 따라 Froude 수와 수력도약 높이비를 분석한 결과, Froude 수가 증가함에 따라 수력도약 높이비가 증가하는 양상을 보였다. 수력도약 높이비는 퇴적토가 있을 경우가 퇴적토가 없을 경우보다 전반적으로 크게 나타났으며, Froude 수가 작더라도 하류부로 이동한 퇴적토의 증가에 따른 하류부 수심의 영향으로 수력도약 높이가 증가된 것으로 판단된다. 따라서 토사의 이동을 수반한 수력도약 높이의 산정에는 토사의 이동특성을 나타낼 수 있는 변수를 도입이 필요한 것으로 판단된다.
3)수력도약 길이비는 Froude 수 3.0 이하에서는 퇴적토 유무와 관계없이 유사하게 증가하는 양상을 보였으나, Froude 수 3.0 이상에서는 퇴적토가 있을 경우 수문 하류로 배출된 퇴적토의 영향으로 수력도약 길이비가 감소하는 것으로 나타났다. 이는 Froude 수에 따른 퇴적토 이동량비에서와 같게 수문 하류로 배출된 퇴적토의 영향으로 수력도약 길이에 영향을 미치는 것으로 판단된다.
4)유량계수 회귀식은 퇴적토 이동현상을 고려하지 않을 경우 수문 직상류의 수심비와 개방도 높이비의 함수로 나타나며, 퇴적토 이동을 고려할 경우 수문 직상류 수심비, 퇴적토이동거리비와 퇴적토 이동량비의 함수로 나타난다. 유량계수 회귀식의 결정계수는 0.749, NSE는 0.774, RMSE는 0.032, MAPE는 8.000%로 나타났다.
5)수력도약 높이 회귀식은 퇴적토 이동현상을 고려하지 않을 경우 수문 직상류의 수심비와 퇴적토높이비의 함수로 나타나며, 퇴적토 이동을 고려할 경우 수문 직상류 수심비, 퇴적토 높이비와 이동량비의 함수로 나타난다. 수력도약 높이 회귀식의 결정계수는 0.896, NSE는 0.853, RMSE는 0.012 m, MAPE는 11.090%로 나타났다.
6)수력도약 길이 회귀식은 퇴적토 이동현상을 고려하지 않을 경우 수문 개방비와 퇴적토이동량비의 함수로 나타나며, 퇴적토 이동을 고려할 경우 수문 개방비, 퇴적토 높이비와 이동량비의 함수로 나타난다. 수력도약 길이 회귀식의 결정계수는 0.915, NSE는 0.984, RMSE는 0.120 m, MAPE는 11.270%로 나타났다.
7)유량계수, 수력도약 높이와 길이에 대한 회귀식의 산정값에 대한 95% 예측구간에는 약 94%에서 100%가 포함되어 개발한 회귀식의 사용성을 확인하였다.
8)유량계수, 수력도약 높이와 길이에 대한 제시한 회귀식의 유의성을 검정 결과, 유의확률이 모두 0.000으로 유의수준 0.05보다 작게 나타났고, 사용된 매개변수의 적정성을 검토하기 위하여 다중공선성을 분석한 결과 다중공선성은 없는 것으로 분석되었다.