1. 서 론
개수로의 바닥전단응력은 국내 설계기준에서는 일반적으로 소류력으로 표현되며 홍수시 하천의 안정성을 평가하는 주요 설계인자이다. 단면의 횡방향 바닥전단응력의 분포는 단면의 유속분포, 이차류, 난류구조 등의 영향을 받는데 복단면 개수로의 경우에는 저수로와 홍수터 간의 유속 차이와 이에 따른 이차류 및 난류구조의 영향으로 매우 복잡한 양상을 나타낸다 (Prinos et al. 1985, Tominaga and Nezu 1991).
복단면 수로의 흐름과 난류 특성은 실험 연구를 통해서 정밀하게 측정되어 제시되었다. Tominaga and Nezu (1991), Shiono and Knight (1991) 등은 LDA (laser doppler anemometers)를 이용한 복단면 흐름 측정에 의해 복단면 형상과 홍수터 조도가 주흐름 분포, 이차류 분포, 레이놀즈 응력 분포, 바닥전단응력, 운동량 교환 등에 미치는 영향을 분석하였다.
복단면 흐름에 대한 수치모의 연구도 최근까지 다양하게 진행되었다. RANS (Reynolds averaged Navier Stokes equations)에 기반한 연구는 Naot et al. (1993), Pezzinga (1994), Sofialidis and Prinos (1998) 등이 대표적인데 이들 연구에서는 자신들의 RANS 모형이 복단면 흐름에서 시간 평균 유속 분포와 바닥 전단응력을 잘 예측하고 있음을 보여준다. Pezzinga (1994)와 Sofialidis and Prinos (1998) 등은 비선형 난류 모형을 이용하여 이차류 분포까지 예측하였다. RANS 모형에 대한 대안인 LES 모형은 큰 규모의 와류를 모델링 없이 직접 해석하므로 난류 이차항에 대한 정확한 계산이 가능하다. 개수로에서 LES를 적용한 대표적이 연구는 Constantinescu et al. (2009), van Balen et al (2010), Stoesser et al (2010) 등이 있다. 복단면 개수로에는 Thomas and Williams (1995)가 처음으로 LES를 적용하였으며 Cater and Williams (2008)는 Thomas and Williams (1995)의 연구를 마무리하였다. Kara et al. (2012)은 Hydro3D 코드를 이용하여 균일 격자로 LES 모의를 수행하여 홍수터 수심에 따른 영향을 검토하였다.
본 연구에서는 복단면 형상에 따른 바닥전단응력 분포를 분석하기 위하여 오픈 소스 코드인 OpenFOAM LES를 이용하여 벽 부근이 조밀한 비균일 격자를 구성하여 모의하였다. 복단면 개수로에서 OpenFOAM 코드의 LES 검증은 Lee (2017)에 의해 수행되어 본 논문에서는 제외하였다.
2. 연구 방법
2.1 지배방정식
LES 지배방정식은 Navier-Stokes 방정식을 공간 필터로 평균하여 구한다. 흐름 변수 (f)는 큰 규모 (large scale)와 작은 규모 (small scale)로 다음과 같이 분리한다.
| $$f=\overline f+f'$$ | (Eq. 1) |
여기서 윗줄표식은 공간 평균된 큰 규모의 흐름 변수이며 프라임은 작은 규모의 흐름 변수이다.
공간 필터를 적용하면 연속방정식과 운동량방정식은 각각 다음과 같다.
| $$\frac{\partial u_i}{\partial x_i}=0$$ | (Eq. 2) |
Eq. 3의 이송항은 항으로 표현할 수 없으므로 SGS (sub grid scale) 응력 텐서를 도입하며 다음과 같이 정의된다.
Eq. 4를 Eq. 3에 대입하면 Eq. 5를 유도할 수 있다.
| $$B_{ij}=\overline{u_iu_j}-\overline{u_iu_j}$$ | (Eq. 4) |
Eq. 5를 풀기 위해서는 SGS 응력 Bij에 대한 모형화가 필요한데 OpenFOAM을 비롯한 다목적 CFD 코드에서는 일반적으로 Boussinesq 가정을 도입하여 모형화한다. 즉, SGS 응력은 점성응력과 유사하다고 가정하며 Eq. 6과 같이 표현된다.
| $$B_{ij}=\frac13B_{kk}\delta_{ij}+\nu_{sgs}\left(\frac{\partial\overline{u_i}}{\partial x_j}+\frac{\partial\overline{u_j}}{\partial x_i}\right)$$ | (Eq. 6) |
여기서 는 SGS 점성이라고 불리며 여과된 속도장에서 계산된다.
SGS 점성을 계산하기 위한 다양한 모형이 제안되었다. Ban and Choi (2014)를 포함한 개수로 흐름 분석에는 Smargorinsky-Lilly SGS 모형이 적용되었다. Rogallo and Moin (1984)에 의하면 Smargorinsky-Lilly SGS 모형은 적용되는 모형 상수 Csgs에 영향을 크게 받으며 특히 벽 부근에서는 난류의 비등방성으로 상수 값이 달리 적용하여야함을 밝혔다. 이를 해결하기 위하여 SGS 난류 운동 에너지의 이송을 고려하는 일방정식 모형이 제안되었으며 본 연구에서는 일방정식 모형을 적용하였다. 일방정식 모형에서 SGS 점성은 Eq. 7과 Eq. 8에 의해 계산된다.
| $$\nu_{sgs}=C_k\triangle\sqrt{k_{sgs}}$$ | (Eq. 8) |
여기서 는 여과 응력 변화율 텐서이며, =1.048, Ck=0.094 이다.
2.2 OpenFOAM 모형 적용
OpenFOAM 모형은 앞에서 제시된 지배방정식을 유한체적법을 적용하여 해석하며 병렬 연산을 위해서 MPI (message passing interface)를 적용한다. 본 연구에서는 MPI를 이용한 병렬 연산을 적용하여 LES 해석을 수행하였다. 유속-압력 상관관계 계산에는 PIMPLE 알고리즘을 적용하였다.
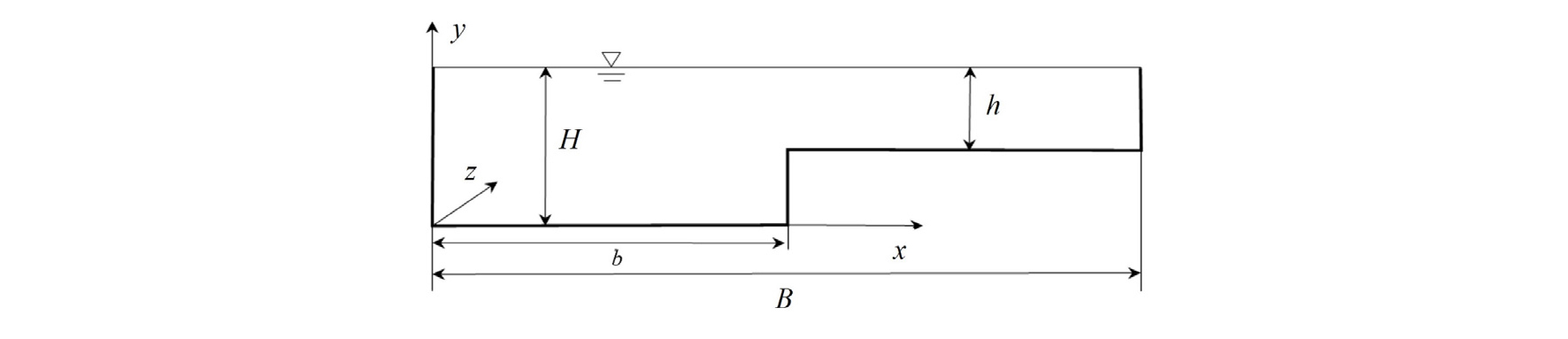
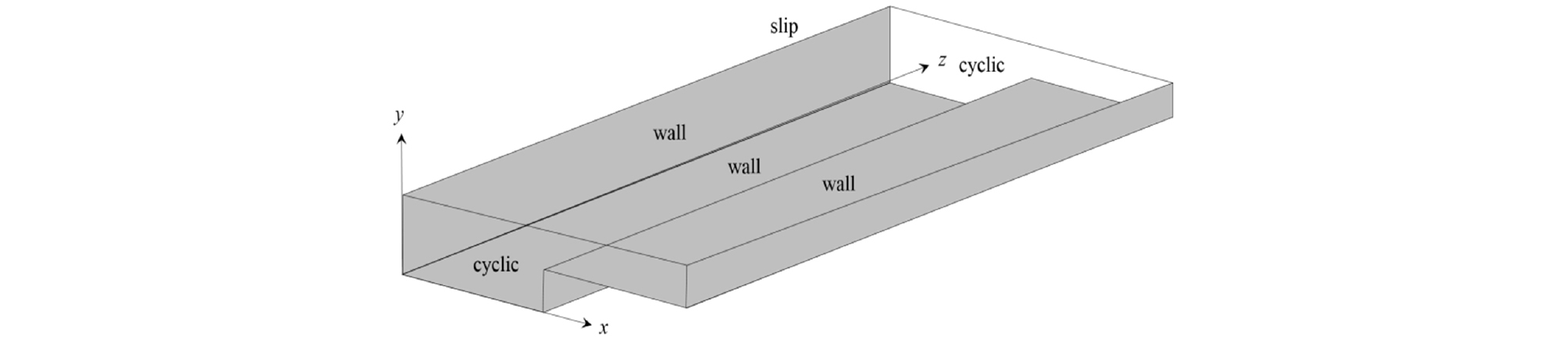
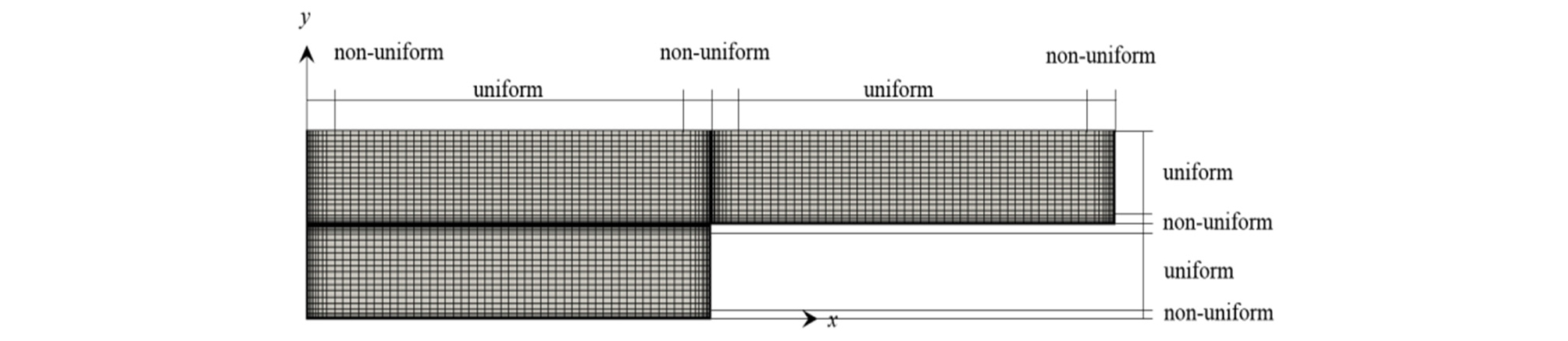
복단면 하도의 변수 정의는 Fig. 1과 같은데 주수로 수심(H)과 전체 하폭(B)은 고정한 상태에서 홍수터 수심(h)과 주수로 폭(b)을 조정하여 총 12개 케이스를 설정하였다 (Table 1). 경계조건은 Fig. 2와 같은데 측벽과 바닥벽은 벽 경계를 적용하였으며 자유수면 경계조건은 free slip 조건을 적용하였다. 계산 영역의 길이는 주수로 수심의 6배로 설정하였으며 상하류 경계는 압력차가 일정한 cyclic 조건을 적용하였다. 계산영역의 격자구성은 Fig. 3과 같으며 x 방향으로 128개, z 방향으로는 128개로 고정하였으며 y 방향으로는 수심에 따라 56-66개의 격자를 구성하였다. 바닥벽과 측벽 부근의 격자가 조밀한 비균일 격자를 적용하였다. 벽 부근의 격자를 조밀하게 구성하여 벽 부근에 발생하는 작은 와를 직접 모의하여 모의의 정확도를 향상시키고자 하였다. 초기 조건으로는 전체 계산 영역에 평균 유속을 설정하였으며 계산 시간이 진행되면서 난류가 발생되도록 하였다. 초기 160 시간 동안 균일한 난류 발생을 위해 모의하였으며 그 이후 30 시간 동안의 모의 결과를 이용하여 난류 특성을 분석하였다.
Table 1. Flow conditions of the simulation cases in this study
계산은 한국건설기술연구원의 클러스터 시스템인 Garam을 이용하였다. Garam은 12개의 계산 노드가 있으며 각 노드는 20개의 코어로 구성되어 있어 총 240개의 코어를 병렬로 사용할 수 있다. CPU는 Intel Xeon E5-2680v2 2.8GHz이며 운영체제는 CentOS이며 OpenFOAM 4.0을 이용하여 계산하였다.
3. 결과 및 논의
3.1 평균 유속 분포
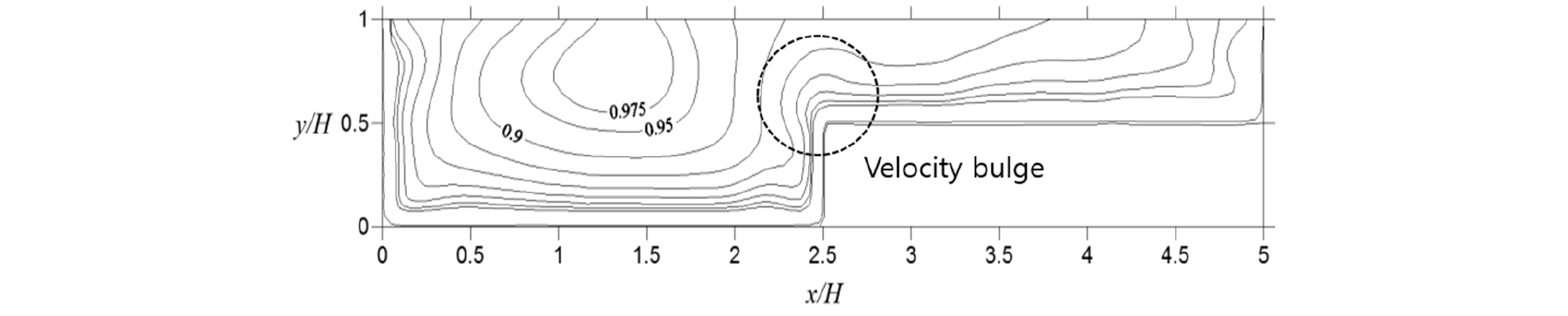
본 논문에서 평균 유속은 시간 동안의 각 지점별 시간 평균 유속을 나타낸다. Fig. 4, Fig. 5 및 Fig. 6은 12개 케이스 중 3개 케이스의 평균 유속 분포를 최대 유속(Umax)으로 나눈 분포를 나타내고 있다. 유속처짐 (velocity dip) 현상은 홍수터 수심이 얕은 경우에 보다 확실하게 나타나고 있다. 유속처짐 현상은 기본적으로 측벽의 영향으로 인해 발생하므로 홍수터 수심이 얕은 경우는 홍수터 연결부의 주수로 측벽 영향이 증가된다고 볼 수 있다. 즉, 홍수터 수심이 얕은 경우에는 단단면과 유사한 유속분포가 나타난다. 홍수터의 수심이 깊은 경우에는 폭이 넓은 직사각형 수로의 유속 분포와 유사하게 나타난다. 즉, 홍수터 연결부의 측벽 영향은 상당히 약해지며 바닥의 영향이 지배적임을 나타낸다.
홍수터 수심이 증가함에 따라 최대 유속 발생 지점이 홍수터 방향으로 이동하는 것도 확인할 수 있다. 홍수터 연결부에서는 유속분포 상의 등유속선이 자유수면 방향으로 상승하는 분포를 나타내는데 이를 유속분포 볼록화 (velocity bulge)라 부른다(Fig. 4 참고). 이 현상은 홍수터의 수심이 깊은 경우에는 뚜렷하게 관찰되나 홍수터 수심이 얕은 경우에는 약해진다.
3.2 이차류 분포
Tominaga and Nezu (1991)는 실험 결과에 의해 복단면 하도에서 총 5 가지 와류를 관찰하여 제시하였다. 자유수면와류 (free surface vortex)는 주수로에서 발생하는 시계방향 와류이며 주수로와류 (main channel vortex)는 홍수터와 인접한 주수로에 발생하는 반시계 방향 와류이다. 홍수터 와류 (floodplain vortex)는 주수로에 인접한 홍수터에서 발생하는 시계 방향 와류이며, 바닥 와류 (bottom vortex)는 주수로 바닥벽에서 발생하는 반시계 방향 와류이며, 연결부 바닥 와류 (junction bottom vortex)는 홍수터 연결부의 주수로 바닥에서 발생하는 시계 방향 와류이다.
Fig. 7, Fig. 8및 Fig. 9는 대표 케이스에 대한 이차류 분포를 나타내고 있다. 이차류 분포는 수심이 동일한 경우에는 하폭에 따른 영향을 받지 않고 모든 케이스에서 유사한 분포를 나타내고 있다. 즉, 홍수터 연결부에서의 주수로 와류와 홍수터 와류의 양상이 비슷하게 나타난다.
홍수터 폭 변화에 따라 홍수터 와류는 다른 양상을 나타낸다. h/H = 0.5에서는 홍수터 폭이 넓은 경우에는 2-3개의 홍수터 와류 구조가 나타나지만 홍수터 하폭이 감소하면 홍수터 와류가 1개로 감소하며 홍수터 측벽의 내부 와류가 명확하게 관찰되지 않는다.
h/H = 0.25에서도 비슷한 양상이 나타나는데 홍수터 하폭이 감소하면서 홍수터 와류의 개수가 감소하며 홍수터 측벽의 내부 와류가 명확하게 나타나지는 않는다. 주수로의 와류 구조는 주수로 폭이 증가하면서 보다 복잡한 양상을 나타내고 있다.
h/H = 0.75인 경우에는 홍수터의 와류구조가 복잡한 양상을 나타낸다. 홍수터 폭이 넓은 CR21에서는 홍수터 중앙에 큰 규모의 홍수터 와류가 나타나며 홍수터 측벽에 3개의 내부 와류가 명확하게 나타난다. 홍수터 폭의 감소에 따라 홍수터 중앙의 와류 규모는 감소하며 홍수터 측벽의 내부 와류와 결합하는 형태를 나타낸다. 홍수터 폭이 최소가 되는 CR24에서는 1개의 홍수터와 와류와 2개의 측벽 내부 와류만이 명확하게 나타난다.
3.3 바닥전단응력 분포
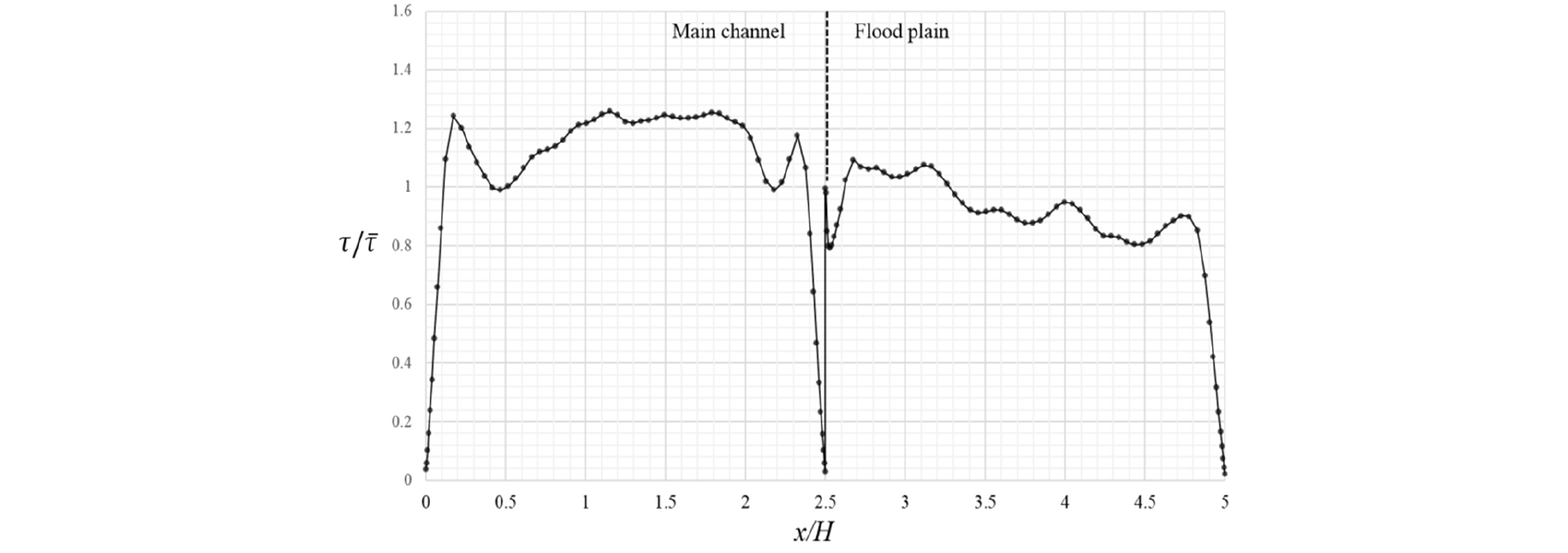
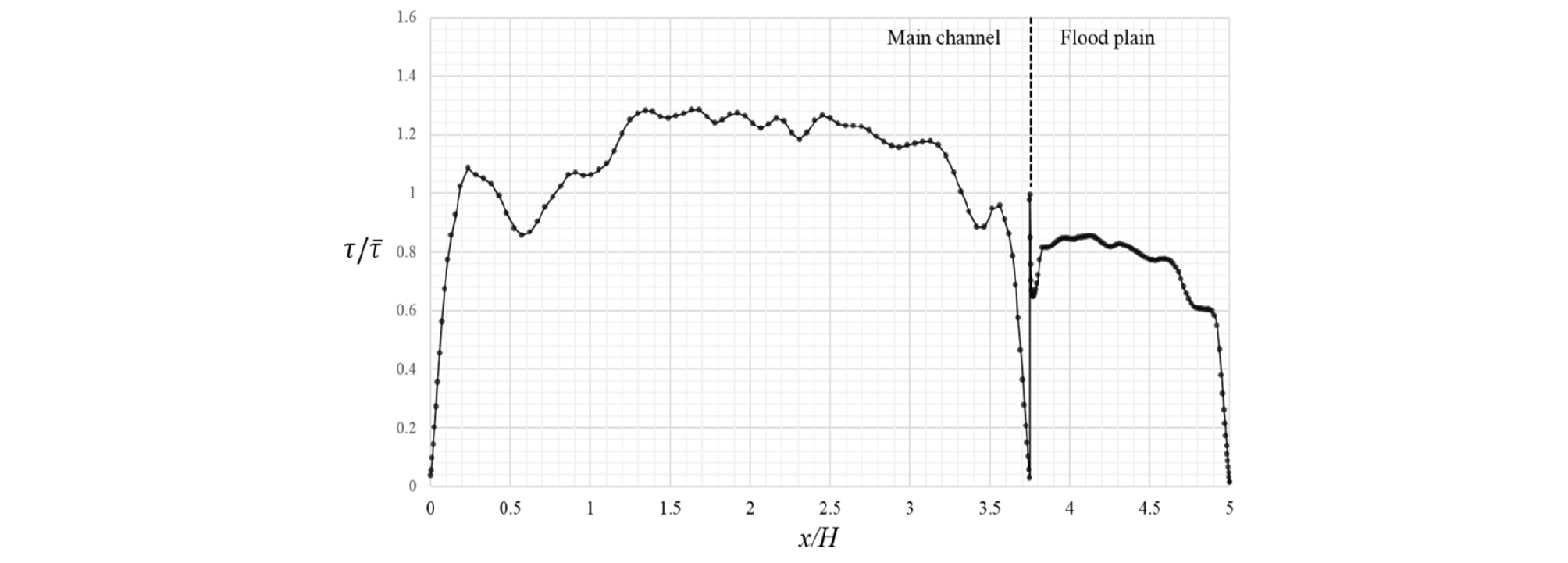
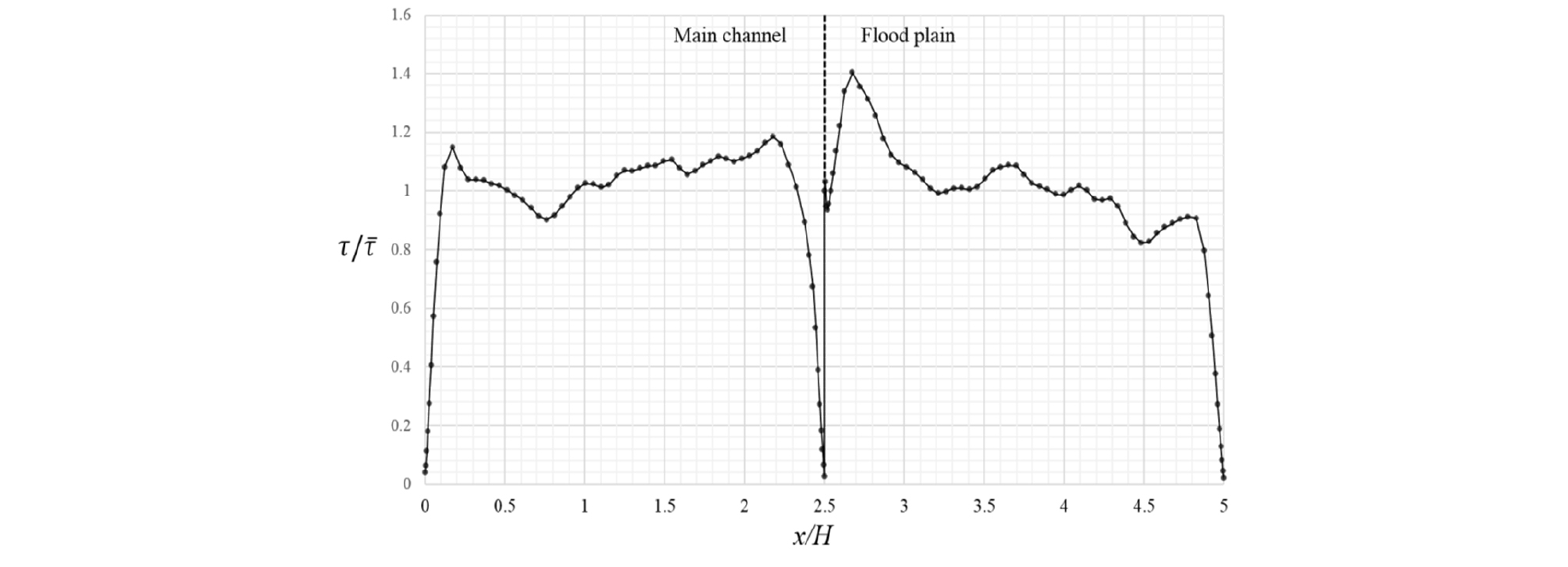
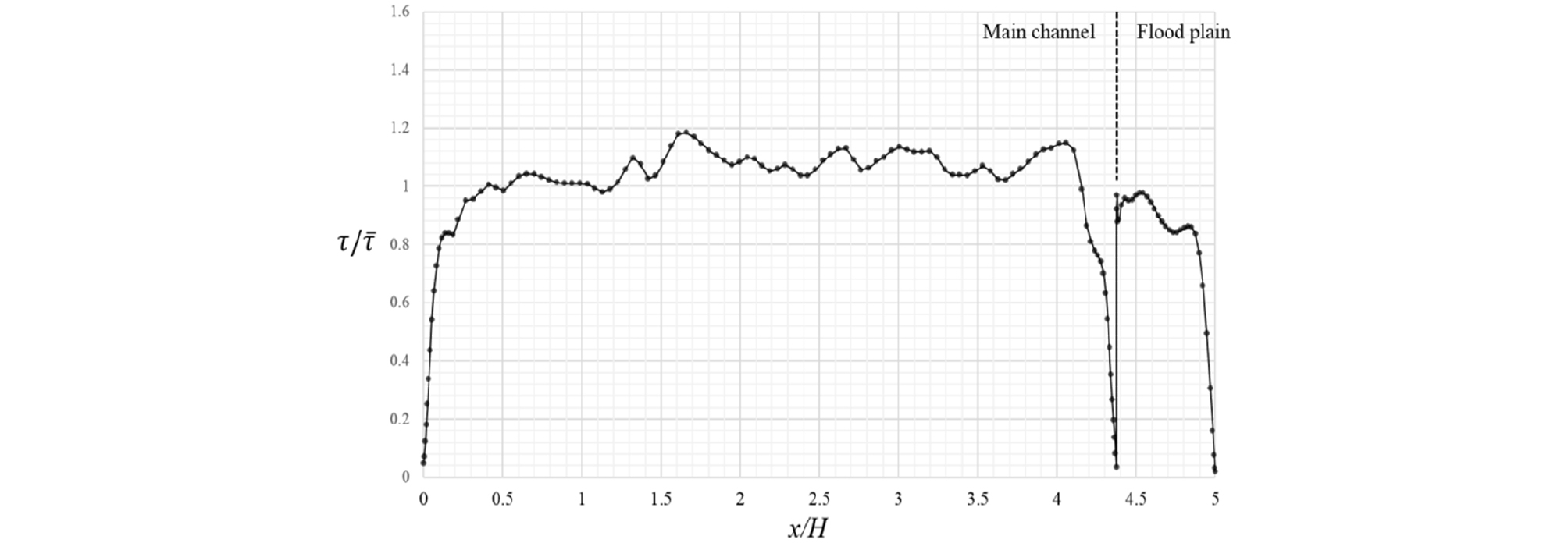
Fig. 10 – Fig. 15는 대표적인 케이스에 대한 횡방향 바닥전단응력 분포를 나타내고 있는데 이 분포는 평균 전단응력에 대한 각 지점의 전단응력의 비를 나타낸다. 전체적인 바닥전단응력의 분포는 주수로에서 높은 값과 홍수터에서의 낮은 값을 나타내는 일관성을 보여주고 있다. 바닥전단응력의 국부적인 변화는 이차류 방향과 관련이 있는 것으로 알려져 있다(Tominaga and Nezu 1991).
h/H = 0.5에서는 주수로 측벽, 주수로 중앙, 홍수터 연결부, 홍수터 좌안, 홍수터 측벽 등에서 높은 값을 나타낸다. CR01에서는 최대값은 주수로 중앙에서 나타나지만 주수로 측벽에서도 주수로 좌안 측벽의 내부 와류의 영향으로 높은 값을 나타내고 있다. 홍수터의 바닥전단응력 분포는 홍수터 연결부 부근에서 높은 값을 나타내며 우안 방향을 따라 감소하는 경향을 보여주고 있다. 홍수터 폭이 감소함에 따라 주수로의 바닥전단응력이 상대적으로 증가하며 홍수터의 전체적인 바닥전단응력은 감소하는 경향을 뚜렷이 나타내고 있다. 홍수터 폭이 가장 작은 CR04에서 홍수터의 최대 소류력은 평균 소류력의 0.8 배 정도로 나타난다.
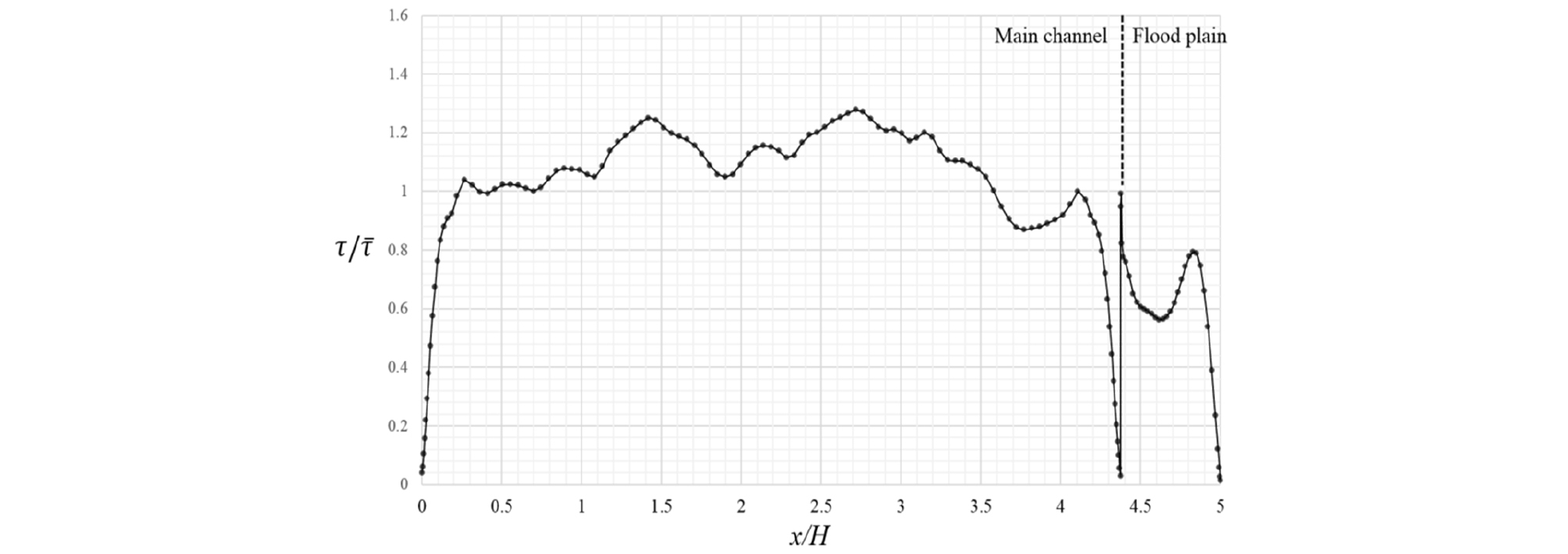
h/H = 0.25에서는 홍수터 수심이 얕아서 흐름이 주수로에 집중되므로 주수로에서의 바닥전단응력이 높게 나타난다. 주수로 중앙에서도 높은 바닥전단응력이 나타나지만 주수로의 우안에서도 높은 값이 나타난다. 이는 홍수터 연결부의 측벽 높이가 높아서 측벽에 의한 이차류 영향을 상당히 받고 있음을 보여준다. 홍수터에서의 바닥전단응력분포는 홍수터 좌안에서 높은 값을 나타내며 우안 방향을 따라 감소하는 경향을 나타내고 있다. 그러나 홍수터 폭이 매우 좁은 경우에는 홍수터 우안 측벽에서 발생하는 이차류의 영향으로 국부적으로 높은 값을 나타내고 있다. CR11를 제외하고 홍수터의 최대 바닥전단응력은 평균전단응력의 0.8 배 정도로 나타나고 있다.
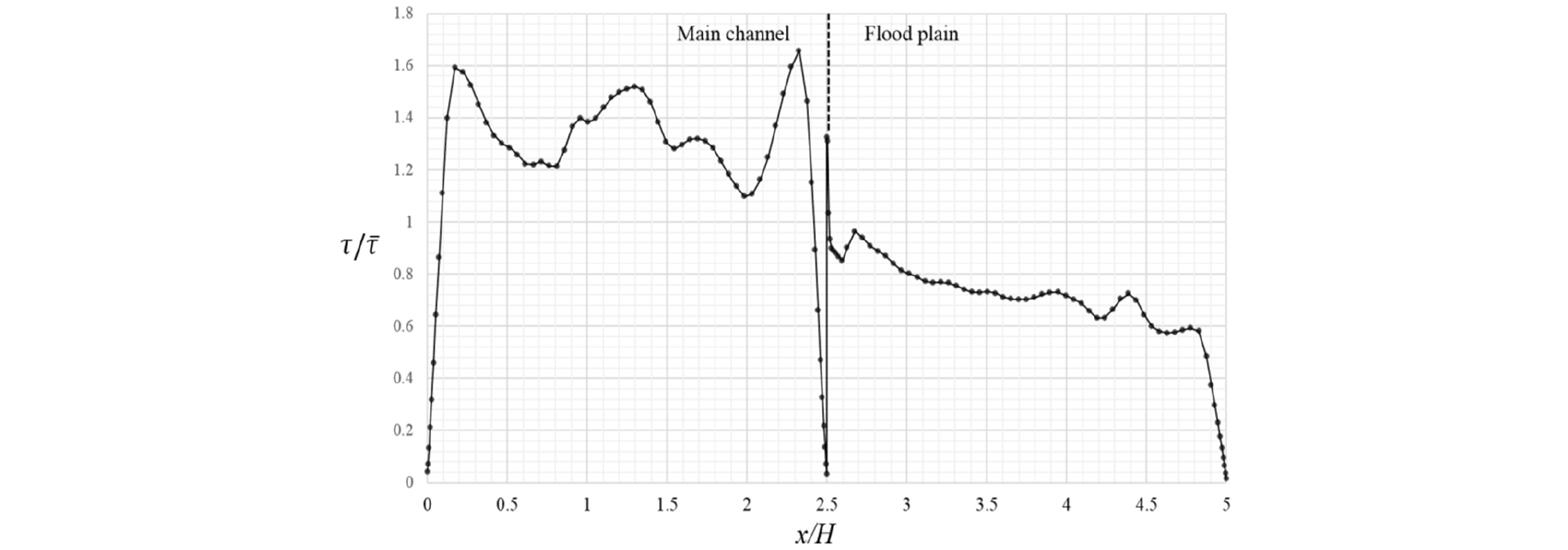
h/H = 0.75인 경우에는 복잡한 이차류 구조로 인하여 바닥전단응력의 분포도 다소 복합적인 양상을 나타낸다. 홍수터의 높이가 수심이 비해서 낮으므로 홍수터의 바닥전단응력이 높게 나타나며 국부적으로 홍수터 연결부의 이차류 구조로 인하여 최대 전단응력이 홍수터에서 발생하기도 한다. 반면에 홍수터 우안 측벽에 의한 국부적인 바닥전단응력의 상승이 나타나기는 하지만 그 크기는 제한적이다. 홍수터 폭이 감소함에 따라 홍수터의 바닥전단응력은 감소하는데 홍수터 폭이 가장 작은 CR24에서는 큰 폭의 감소 경향을 나타내고 있다. 그러나 홍수터의 바닥전단응력은 h/H = 0.25와 0.5에 비해서는 큰 편으로 그 값이 가장 작은 경우에도 평균전단응력의 1.0 배에 근접하고 있다.
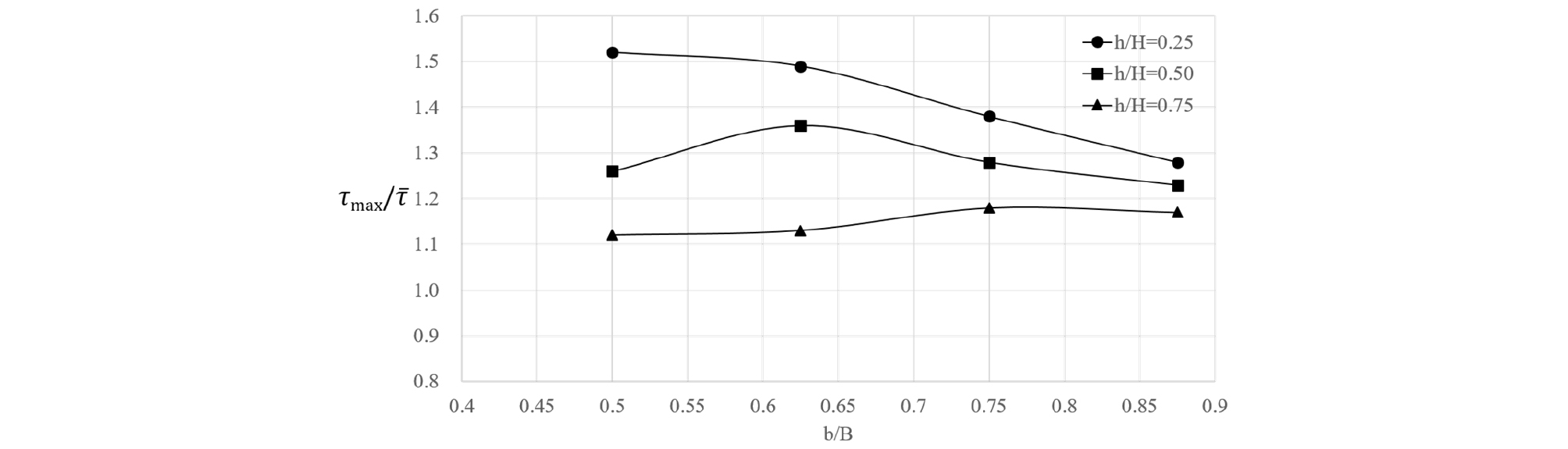
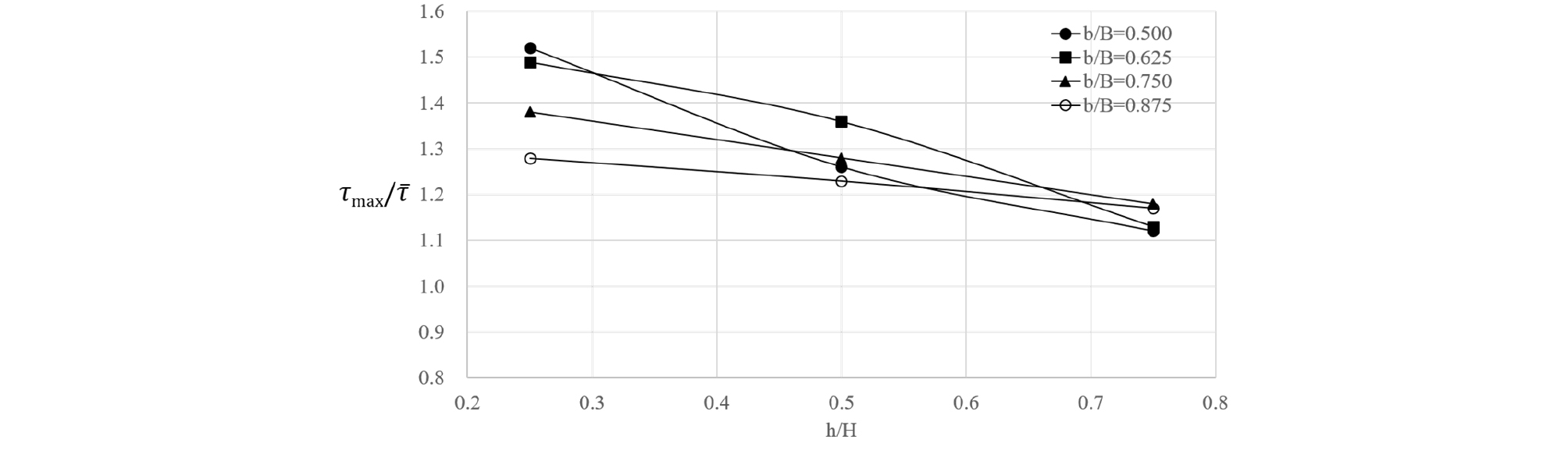
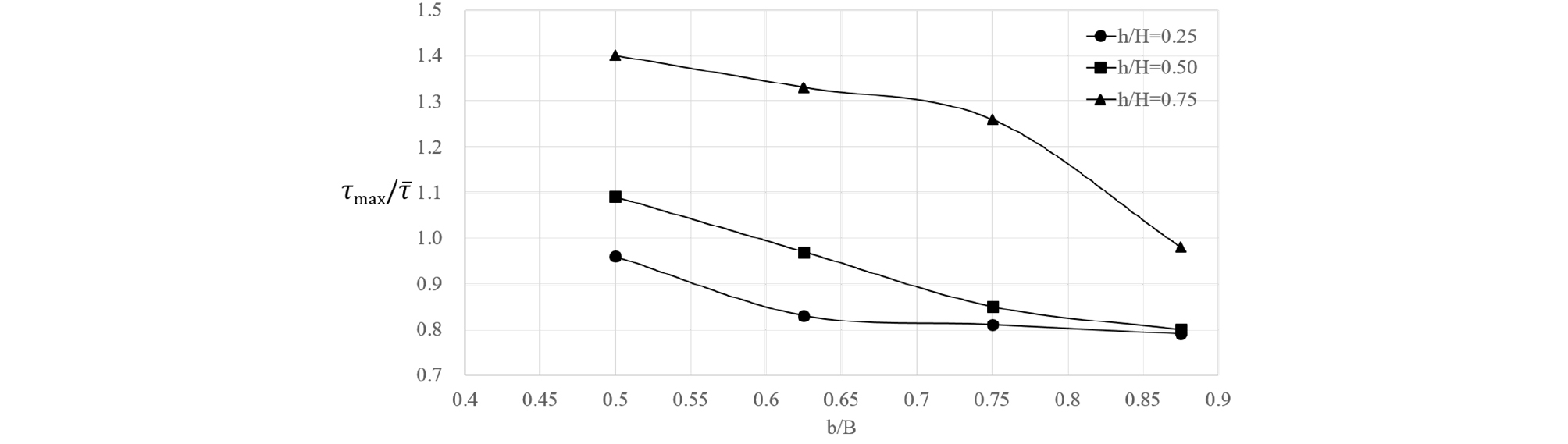
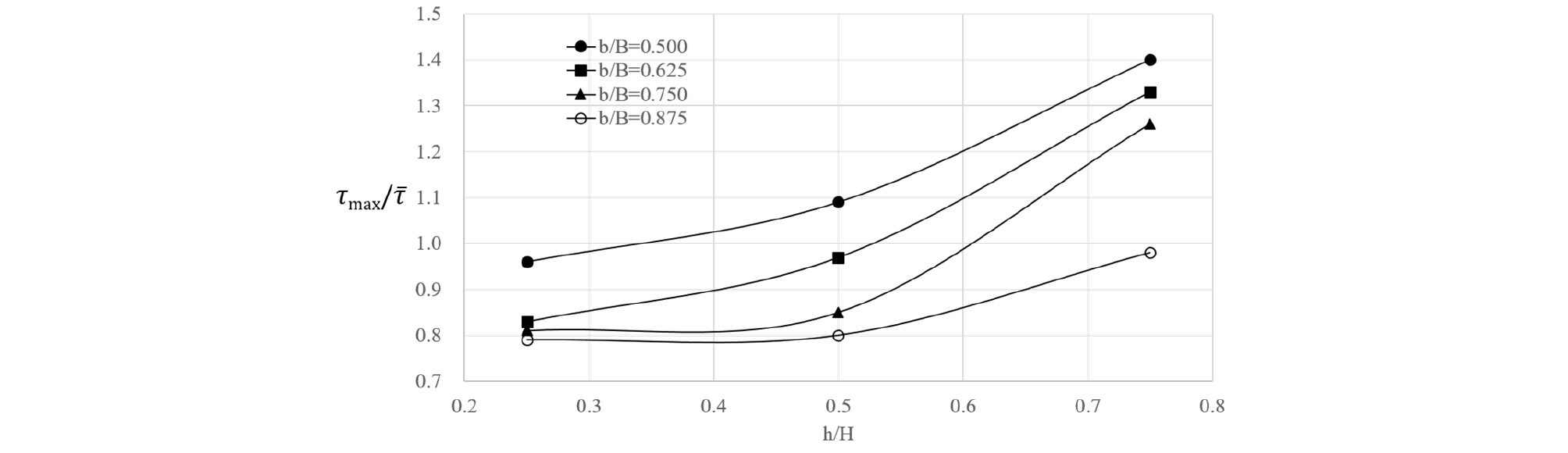
모의된 케이스에 대해서 주수로와 홍수터에서 수심비(h/H)와 하폭비(b/B)의 변화에 따른 최대 바닥전단응력을 비교하면 Fig. 16 – Fig. 19와 같다. 수심비가 증가하면 최대 전단응력은 주수로에서는 감소하나 홍수터에서는 증가하는 양상을 나타낸다. 하폭비 증가에 따른 양상은 주수로에서는 수심에 따라 다소 감소하거나 증가하는 양상을 나타낸다. 홍수터에서는 하폭비 증가에 따라 최대 전단응력은 감소하는 경향을 나타낸다.
4. 결 론
본 연구에서는 홍수터 안정성 분석을 위하여 복단면 하도의 바닥전단응력의 분포를 홍수터 수심과 하폭 변화에 따라 모의하여 분석하였다. 바닥전단응력의 분포는 주흐름과 함께 이차류의 영향을 크게 받으므로 이를 고려하기 위하여 OpenFOAM의 LES 모형을 이용하여 모의하였다. 홍수터 침수의 다양한 조건을 고려하기 위하여 하폭과 수심 조건에 따라 12가지 조건을 설정하여 모의를 수행하였다. 모의 결과를 이용하여 복단면 형상에 따른 시간평균 유속분포, 이차류 분포, 바닥전단응력 분포 특성 등을 분석하였다.
시간 평균 유속분포에 의해 홍수터 형상에 따른 최대 유속 처짐 현상과 홍수터 연결부 유속분포 볼록화 현상의 변화를 관찰할 수 있었다. 이차류 변화는 홍수터가 좁고 얕은 경우에는 홍수터 와류 구조가 단순해지며 홍수터 측벽의 영향은 일정 정도 유지됨을 확인할 수 있었다.
홍수터 바닥전단응력 분포는 전체적으로 홍수터 좌안에서 높은 값이 나타나고 우안 방향으로 감소하는 경향을 확인하였으나 이차류에 의해 상당한 국부적인 변화가 나타남을 확인하였다. 홍수터의 수심이 얕은 경우에는 평균전단응력의 0.8배 이하로 낮은 값이 나타나고 있으나 홍수터의 수심이 깊은 경우에는 평균전단응력의 1.2-1.4배의 높은 값이 나타남을 확인하였다. 홍수터의 폭이 좁은 경우에는 홍수터 우안 측벽의 영향으로 국부적으로 높은 값이 나타나는 것도 확인할 수 있었다.
홍수터 바닥전단응력의 분포는 하천설계에서 홍수터와 제방의 설계 외력을 고려하기 위해 매우 중요하나 국내에서는 관련 연구가 많지 않다. 본 연구는 실제 하천의 조도 상태와 규모를 충분히 반영하지 못한 한계는 있으나 홍수터의 상대적인 수심과 하폭에 따른 설계 소류력의 양상을 참고할 수 있는 자료로 의미가 있을 것으로 기대한다.