1. 서 론

지구 온난화가 가속화되면서 전 지구적인 기후변화가 발생하고 있으며, 이로 인하여 집중호우 및 슈퍼태풍 등 극한기후현상이 빈번하게 발생하고 있다 (Kim et al. 2016). 기후변화는 인간이 쉽게 인지할 수 있는 생태계의 변화뿐만 아니라 사회기반시설에도 여러 모양으로 직․간접적인 영향을 미칠 수 있다 (Ausilio and Conte 2005, Yasuhara et al. 2007, Shahriar et al. 2014, Park et al. 2017). 특히, 기상 및 수문학적 영향으로 인한 지하수위의 변동은 지반의 유효응력에 변화를 일으키고, 결과적으로 기초구조물의 지지력 감소 및 침하 발생과 관련된 문제를 일으킬 수 있다. 그러나 기초구조물 설계에는 지반조사 당시 관측된 지하수위를 고정수위로 간주하고 설계하는 것이 일반적이다 (Kim and Lee 2018). 따라서 기후변화로 인하여 발생하는 점진적인 환경변화 및 급진적인 재난에 대비하고, 기초구조물의 장기간 안전성 및 사용성 개선을 위해서 적절한 지하수위 변동 평가와 예측을 할 필요가 있으며, 그 결과를 기초구조물 건설시 설계단계에서부터 반영할 필요가 있다.

인공신경망 (Artificial neural network, ANN)은 관측된 기상․수문 데이터를 기반으로 지하수위를 예측할 수 있는 데이터처리 방법 중 하나로써 여러 연구자들에 의하여 채택되어 왔다 (Daliakopoulos et al. 2005, Trichakis et al. 2011, Sahoo and Jha 2013). 지하수위를 예측하는 절차와 사용법이 수학과 물리적인 배경으로 제안된 방법 보다 간단하기 때문에 지반공학을 비롯한 여러 공학적 분야에서 사용될 수 있다. ANN은 기본적으로 input layer, hidden layer, 그리고 output layer로 구성되어 있으며, input layer와 output layer에 영향인자들 및 지하수위를 각각 설정하여 input layer와 output layer의 사이에 위치한 hidden layer에서 영향인자들과 지하수위간의 최적 연결강도를 결정 (학습)하는 형태이다. 이렇게 결정된 최적 연결강도는 지하수위 변동에 영향을 미치는 인자들의 값만으로 지하수위의 변동을 예측할 수 있다. Dawson and Wilby (2001)은 ANN을 이용하여 지하수위와 같은 수문학적 요소들을 예측하기 위한 여러 학습 모델들과 예측결과를 정량적으로 평가하는 정리하였으며, Daliakopoulos et al. (2005)는 데이터 학습에 흔히 사용되고 있는 여러 알고리즘을 이용하여 지하수위를 예측하였고, 지하수위 예측에 가장 적합한 학습 알고리즘을 제시 하였다. Sahoo and Jha (2013)는 매우 많은 연구 대상지역을 선정하여 ANN과 선형다중회귀모델과 지하수위 예측 퍼포먼스를 비교 분석하였고, ANN의 지하수위 예측에 대한 우수성을 보였다.

ANN는 관측된 데이터를 기반으로 하는 통계적 방법의 하나이기 때문에 학습에 사용되는 데이터의 질과 양이 예측 결과에 큰 영향을 미칠 수 있으며, ANN의 학습에 사용되는 인풋데이터를 확대하거나 정제하여 지하수위 예측에 사용하는 연구도 사례도 있다 (Makridakis et al. 2008, Seo et al. 2015, Nourani and Mousavi 2016). Seo et al. (2015)는 wavelet decomposition 기술을 이용하여 제한된 input을 여러 개의 인풋으로 확장하여 목표 수문인자를 예측하였으며, Nourani and Mousavi (2016)는 Wavelet transform 기법으로 관측된 영향인자들을 정제하여 학습 및 예측을 위한 input 데이터로 사용하였다. Makridakis et al. (2008)와 Sahoo and Jha (2013)는 ANN을 이용하여 지하수위를 예측하는데 있어서, 계절의 영향을 반영하기 위해 수문학적 관측 데이터 이외의 Dummy라는 input을 추가하였다. 이후 Kim and Lee (2018)은 ANN으로 하천변 도심지역에서 지하수위를 예측하는데 Dummy를 인풋으로 사용되었다. 그러나 ANN을 이용한 지하수위 예측에 있어서, 계절의 영향을 반영하기 위해 도입된 Dummy가 ANN의 예측 퍼포먼스에 어떠한 영향을 미치는지에 대한 연구는 여전히 부족한 실정이다.

본 연구에서는 하천변 도심지역이라는 특정한 지역에서 ANN으로 지하수위를 예측함에 있어서, 계절 영향을 반영하기 위해 도입된 Dummy의 영향을 분석하였다. 분석을 수행하기 위하여, 서울시 마곡동을 연구대상지역으로 선정하였으며, 국가기관으로부터 신뢰할 수 있는 관측데이터를 확보하였다. 그리고 여러 문헌에서 지하수위를 예측하기 위해 자주 사용되는 알고리즘을 차용하였으며, Dummy를 input으로 추가한 경우와 추가하지 않은 경우에 대하여 비교분석 하였다. 정성적 및 정량적 비교분석을 위하여 다양한 도해법 및 상관계수, 에러 인덱스 등을 사용하였다.

2. 연구방법

2.1 연구대상지역

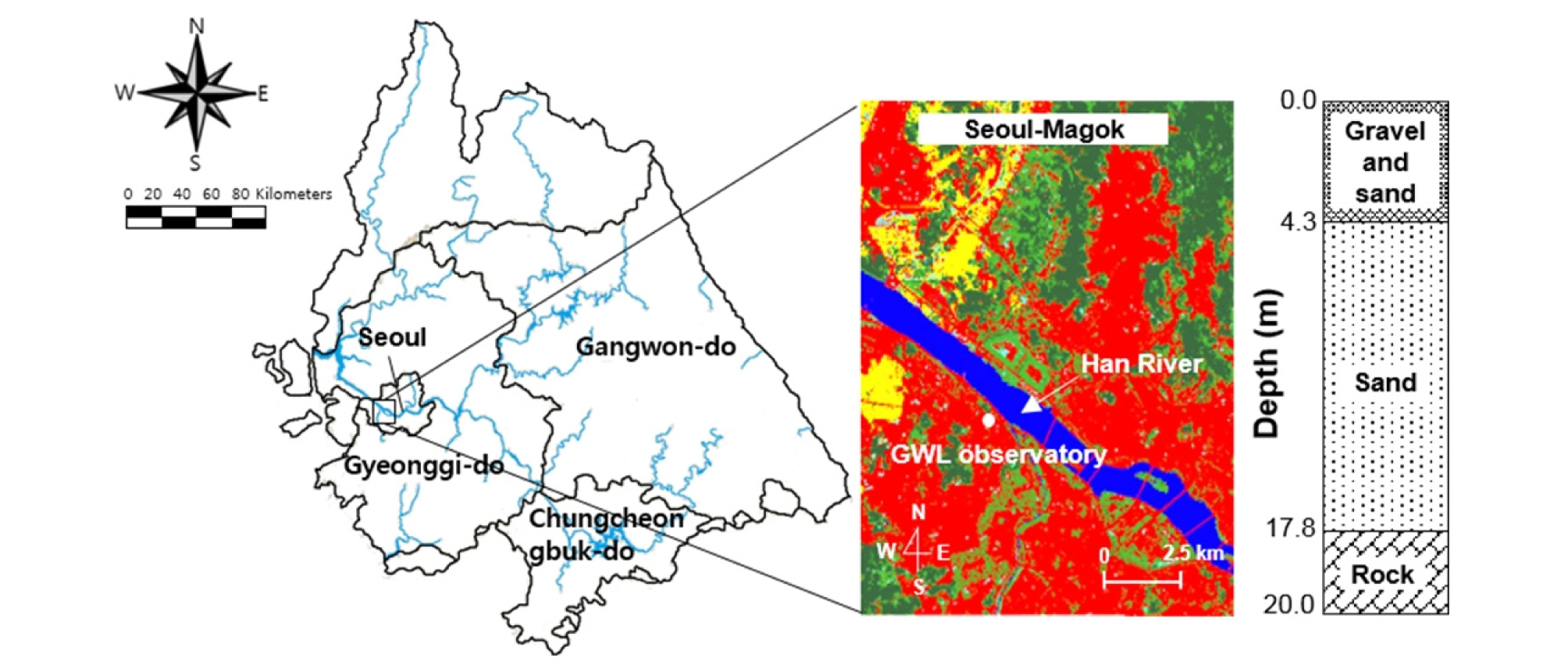
본 연구에서는 하천변에 위치한 도심지역으로써 서울시 마곡동을 대상지역으로 선정하였다. 연구 대상지역은 Fig. 1과 같이 서울의 남서쪽에 위치해 있으며 부근의 경도와 위도는 각각 37˚34´35˝와 126˚50´12˝이다. Fig. 1의 빨간색 표시는 도시화된 지역으로써 불투수 지표면으로 분류되며 대상지역의 대부분이 불투수 지표면인 것을 확인할 수 있다. 이 지역 위로 흐르고 있는 한강은 유역면적이 24,753.2 km², 하폭이 1013 m, 하상경사가 330인 규모가 매우 큰 강이다. 지질상태는 상부층에 자갈섞인 모래가 존재하며 깊이 4.3 m부터 17.8 m까지 모래층이, 그 하부층에는 암반층이 존대한다. 이지역은 대부분 충적층으로 분류되며 투수성이 매우 높은 흙으로 구성되어 있다 (GIDS).

Fig. 1.

The location, surface condition and soil profile of study site.

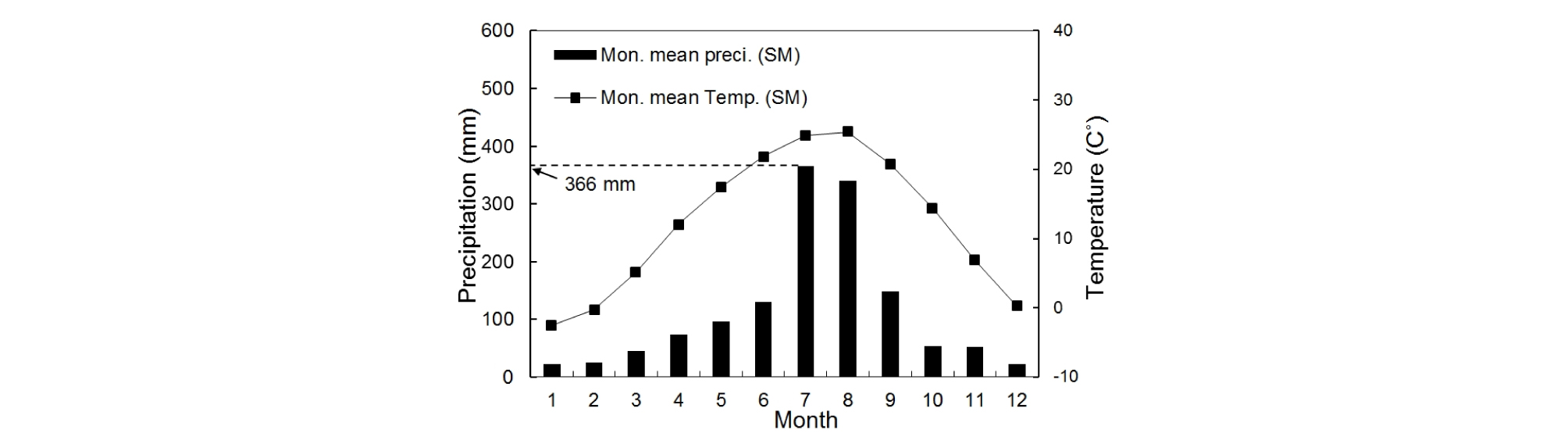
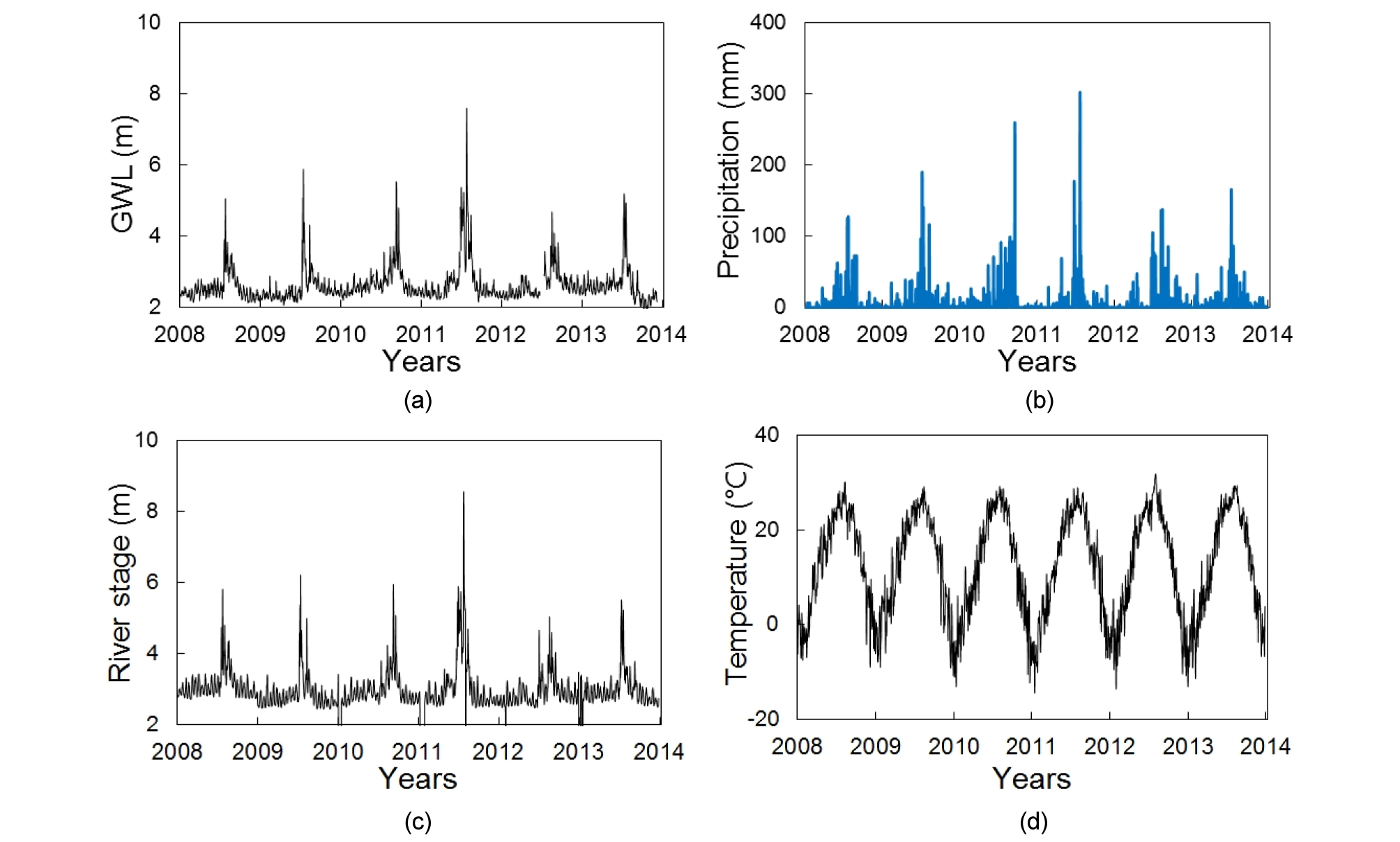
Fig. 2는 대상지역에서 30년간 관측된 월별 평균 강우 및 온도 분포를 보여준다. 이 지역의 연평균 강우량은 약 1,376.5 mm이고, 강우는 대부분 7 - 8월에 집중되어 있으며 7월의 월평균 강우량이 366 mm로 연중 가장 많은 양의 강우가 이 달에 발생한다. 반면, 겨울에는 강우가 거의 발생하지 않는다. Fig. 3은 2008 - 2013년의 6년간 대상지역에서 관측된 지하수위, 강우량, 하천수위 그리고 기온을 나타낸다. Fig. 2와 같이 Fig. 3에서도 강우량이 여름에 집중되어 있는 것을 확인할 수 있으며, 이에 따라 하천수위와 지하수위도 여름에 크게 상승하는 것을 확인할 수 있다. 특히, 2011년에 매우 많은 강우량이 관측되었으며 이시기에 지하수위와 하천수위도 크게 상승하였다. 또한, 기온을 포함한 모든 인자들이 강한 주기성을 보이며 변동하는 것을 확인할 수 있다.

Fig. 2.

Monthly mean precipitation and temperature for study site.

Fig. 3.

Observed meteorological and hydrological data. (a) GWL, (b) precipitation, (c) river stage, (d) temperature.

2.2 인공신경망 (ANN)

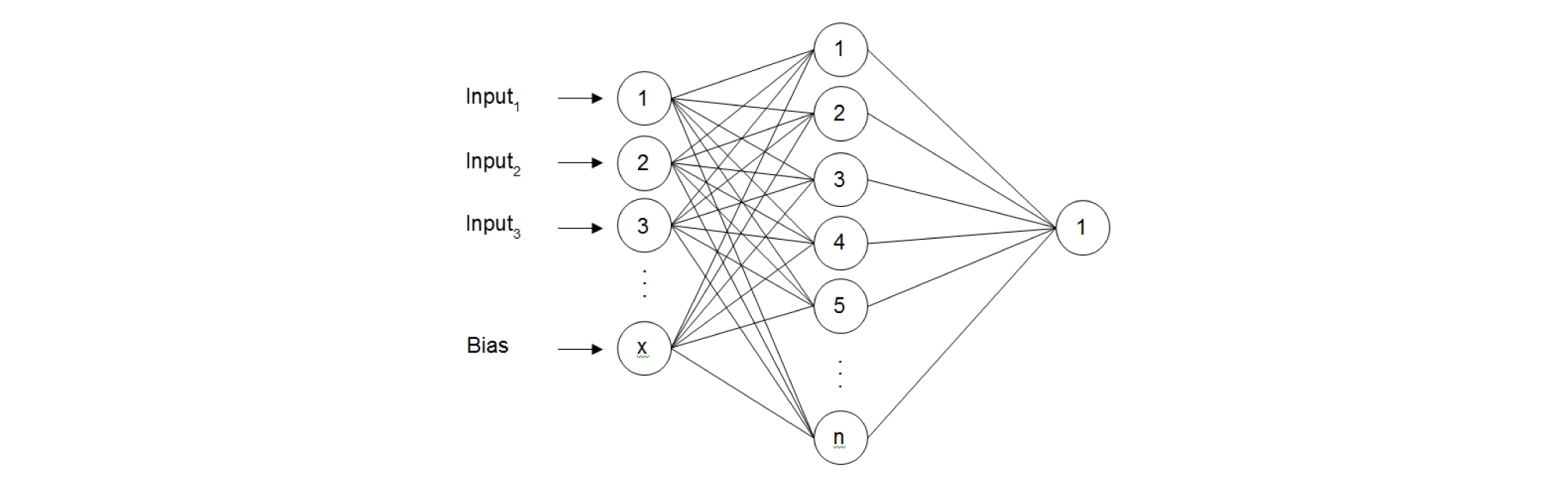
ANN은 지하수위를 예측하는데 빈번히 사용되는 데이터처리 모델 중에 하나이다. Fig. 4에 나타나 있는 것과 같이 ANN의 구조는 input layer, hidden layer 그리고 output layer으로 구성되어 있으며 다음과 같은 식으로 표현될 수 있다.

Fig. 4.

The structure of artificial neural network.

$y_i=F\left(\sum _{i=1}^n{w}_{ij}{x}_i+b\right)$    (Eq. 1)

여기서 x_i와 y_j는 각각 이전 층의 i번째와 현재 층의 j번째 노드값이며, b_j는 현재층의 j번째 노드의 편중값, w_ji는 xi와 y_j의 연결강도, n은 이전 층의 노드 개수, F는 층에 할당된 active fucntion을 나타낸다. ANN에서는 input에 의한 신호가 hidden layer의 hidden node들에 전달되고 이들은 다시 active function을 통해 output으로 출력된다. 이때 출력된 output은 예측하고자 하는 목표 값과 비교하여 적절한 오차범위안에 들어 올 때까지 각 layer와 node간의 연결강도를 수정하여 반복 계산하게 되며 이를 ‘학습 (learning)’ 이라고 한다.

일반적으로 ANN을 이용하여 지하수위를 예측하는 절차는 1) 지하수위 변동에 영향을 미치는 영향인자들의 선정, 2) 지하수위 예측에 적합한 학습모델 선정, 3) 적합한 active function 결정, 4) 최적의 hidden node와 hidden layer 수 결정, 5) 데이터 학습을 통한 최적 연결강도 결정, 6) 지하수위 예측으로 나눌 수 있다. 일반적으로 ANN을 이용하여 지하수위를 예측하는데 기상․수문 자료로써 하천수위, 강우량 그리고 기온 등이 이용된다. 일반적으로 지하수위와 같은 수문 인자들은 input과 output사이에 시간지연이 발생한다. ANN에서는 시간지연의 영향을 반영하기 위한 의도로써, 특정 일의 지하수위를 예측하기 위하여 1 - 4일 전에 관측된 인자들을 인풋으로 사용하는 방법이 빈번히 이용된다. 또한, 계절의 영향을 반영하기 위하여 Dummy를 추가하기도 한다 (Makridakis et al. 2008, Sahoo and Jha 2013). Dummy는 11개 또는 12개의 사용자가 인위적으로 기입하는 input이며 D₁, D₂, ⋯, D₁₂로 표현하며, 1월에는 D₁ 값은 1이며 D₂ - D₁₂의 값들은 0이 되고 2월에는 D₂ 값은 1이며 D₁과 D₃ - D₁₂ 값은 0이 된다. ANN의 학습 알고리즘은 이 규칙적으로 설정된 값들로부터 개월 및 개절 등을 인식하며 그 시기의 수문학적 특성 또한 반영 될 수 있다. ANN에서 주어진 데이터를 학습하는데 여러 알고리즘이 사용되고 있으며, Gradient descent with momentum and adaptive learning rate backpropagation (GDX), Levenberg-Marquardt (LM) 그리고 Bayesian regularization (BR)은 가장 일반적으로 사용되는 학습 알고리즘이다. 이 중 지하수위와 그의 영향인자들의 연결강도를 학습할 때 가장 효율적이고 신뢰성이 높은 모델은 LM 알고리즘인 것으로 알려저 있다 (Daliakopoulos et al. 2005, Sahoo and Jha 2013). 또한, 적절한 active function을 결정해야 한다. Input과 output이 서로 선형적인 관계에 있다면 linear function을 사용하여 적은 계산 용량과 시간으로도 신뢰할 만한 결과를 얻을 수 있으나, 일반적으로 지하수위와 지하수위 변동에 영향을 미치는 인자들은 비선형 관계에 있는 경우가 많으며, input과 output의 비선형을 고려하기 위하여 logistic sigmoid function과 같은 비선형 함수를 active function으로 사용할 수 있다. 다음 식은 linear fucntion과 logistic sigmoid function을 나타낸다.

$F\left(v\right)\frac{1}{1+exp\left(-v\right)}$    (Eq. 2)

$F\left(v\right)=v$    (Eq. 3)

$v=\sum _{i=1}^n{w}_{ij}{x}_i+b$    (Eq. 4)

또한, ANN을 이용한 예측결과는 사용자가 설정한 hidden layer와 hidden node의 수에 따라 다를 수 있다. Trial-and-error 방법은 최적의 hidden layer와 hidden node를 결정하기 위하여 빈번히 사용된다. 용어를 통해 유추할 수 있는 것과 같이, 여러 경우의 수로 hidden layer와 hidden node를 설정하여 예측하고 가장 신뢰성 높은 예측결과를 사용한다.

본 연구에서는 학습을 위하여 Fig. 3의 2008년부터 2012년까지 5년간 관측된 지하수위, 강우량, 하천수위, 온도 자료를 이용하였고, 2013년에 관측된 강우량, 하천수위, 온도 자료를 이용하여 2013년의 지하수위를 예측하였다. 그리고 계절 영향을 반영하는 것으로 알려진 Dummy를 추가하여 지하수위를 예측하였으며, 추가하지 않고 예측한 결과와 비교하였다. 또한 시간지연을 반영하기 위하여 어느 특정일 (t)의 지하수위를 예측하기 위하여 t, t-1, t-2, t-3 그리고 t-4일 등의 관측 영향인자 데이터를 인풋으로 사용하였다. 본 연구에서 사용된 input 구성은 Table 1에 정리하였다. 학습 모델로는 지하수위와 수문학적 인자들의 학습에 가장 일반적이며 효율적이라고 알려진 Levenberg-Marquardt algorithm을 채택하였다. 또한, Table 1에 명시된 input 모델들에 대하여 1 - 10개의 hidden node와 1 - 5개의 hidden layer를 각각 적용하여 (input model 당 50 케이스) 지하수위 예측을 수행하였다. 예측결과의 신뢰성을 정량적으로 평가하기 위하여 상관계수 (r)과 에러의 정도를 나타내는 지표인 RMSE를 사용하였다 (Dawson and Wilby 2001). r의 값은 1에 가까울수록 관측결과와 유사한 경향으로 변동함을 나타내고 RMSE의 값이 0에 가까울수록 예측값의 에러가 작다는 것을 나타낸다.

Table 1. Used input models for predicting groundwater level using ANN

3. 연구결과

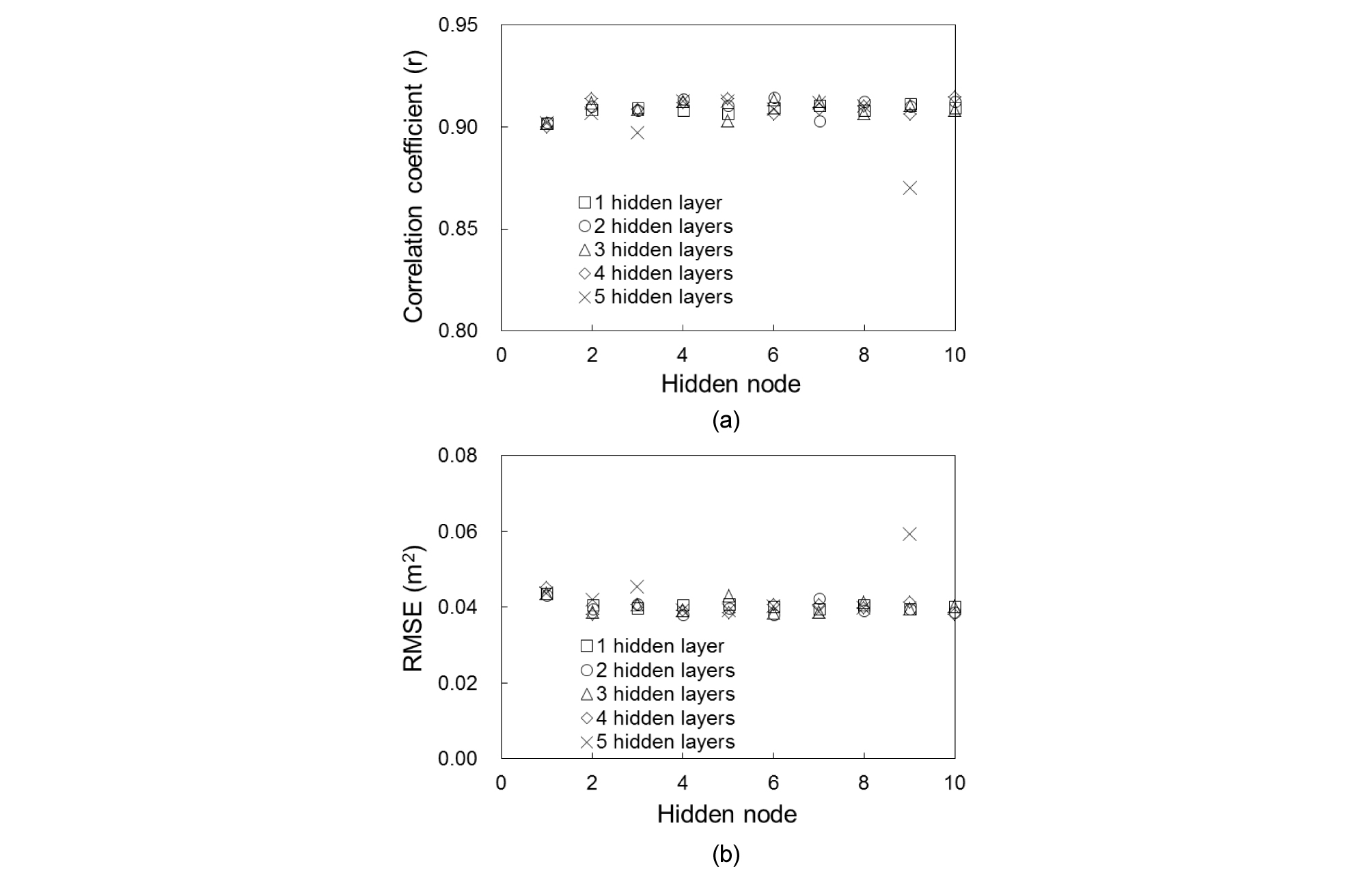
Fig. 5는 Table 1의 input 모델 M1의 hidden node에 따른 지하수위와의 r와 RMSE의 값을 나타낸다. 5 hidden layers의 경우 3과 9의 hidden node에서 튀는 값을 보이지만, 전반적으로 서로 다른 수의 hidden node에 대하여 r과 RMSE의 값은 크게 변하지 않는 것을 확인할 수 있다. 즉, 본 연구에서 사용된 ANN 학습 모델과 대상지역에서는 hidden node의 수가 지하수위 예측 결과에 결정적인 영향을 미치지는 않는 것을 확인할 수 있다. 따라서 편의를 위하여 이후로는 hidden node가 4인 경우의 예측결과만을 선택하여 비교 분석하였다.

Fig. 5.

(a) The correlation coefficient and (b) RMSE values of the predicted GWL with hidden nodes.

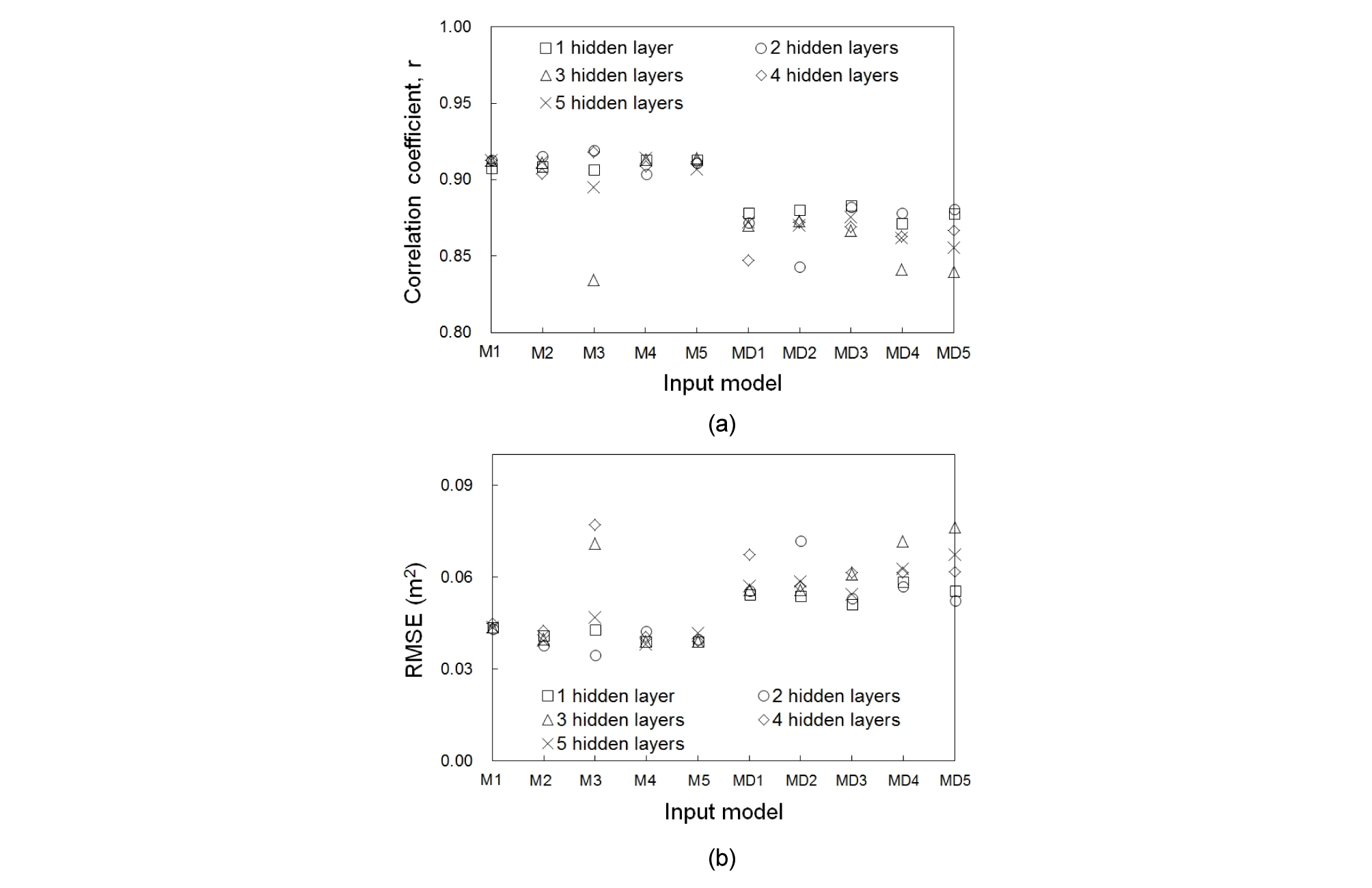
Fig. 6 (a)는 Table 1의 input 모델에 따른 예측 지하수위와 관측 지하수위의 상관계수 (r) 값을 보여준다. 여기서, x축은 각각의 input 모델 명을 나타내며, M1 - M5는 지하수위를 예측하기 위하여 강우량 그리고 하천수위, 기온을 input으로 사용한 모델이며, MD1 - MD5는 계절의 영향을 반영하기 위하여 Dummy를 input에 추가한 모델이다. 또한, Table 1에 나타나 있는 것과 같이 숫자 1 - 5는 지하수위 예측에 시간지연을 고려하기 위하여 추가된 input에 대한 구분이다. Fig. 6 (a)에서 확인할 수 있는 것과 같이 M1 - M5의 r은 대체적으로 0.90 - 0.93 사이의 값을 보이며, MD1 - MD5는 0.83 - 0.88의 값을 보인다. 이 것은 M1 - M5의 input 모델로 예측한 지하수위가 MD1 - MD5의 input 모델로 예측한 지하수위보다 관측된 지하수위 변동 경향을 더 잘 따르는 것을 나타낸다. 또한, M3의 3 hidden layers에서 튀는 것이 관찰되었으며, MD1 - MD5의 모델에서는 4개의 튀는 결과가 관찰되었다. 이를 통해, Dummy를 추가한 경우가 추가하지 않은 경우보다 튀는 결과가 나올 확률이 높은 것을 확인할 수 있다.

Fig. 6 (b)는 input 모델에 따른 RMSE 값을 나타낸다. RMSE의 경향도 r과 같이 Dummy를 인풋으로 추가하지 않은 모델이 Dummy를 추가한 것보다 양호한 결과를 보였다. 즉, Dummy를 사용하지 않았을 때 지하수위 예측결과의 에러가 작은 것을 나타낸다. D1 - D5모델에서 튀는 RMSE가 2개 확인되었으며, MD1 - MD5 모델에서는 비교적 넓은 분포의 RMSE값을 보였다. Fig. 6 (b)를 통하여 Dummy를 사용했을 경우 input 모델과 hidden layer에 따라 튀는 값이 나올 확률이 높은 것을 확인할 수 있다.

Fig. 6.

(a) The correlation coefficient and (b) RMSE values of the predicted GWL with input models.

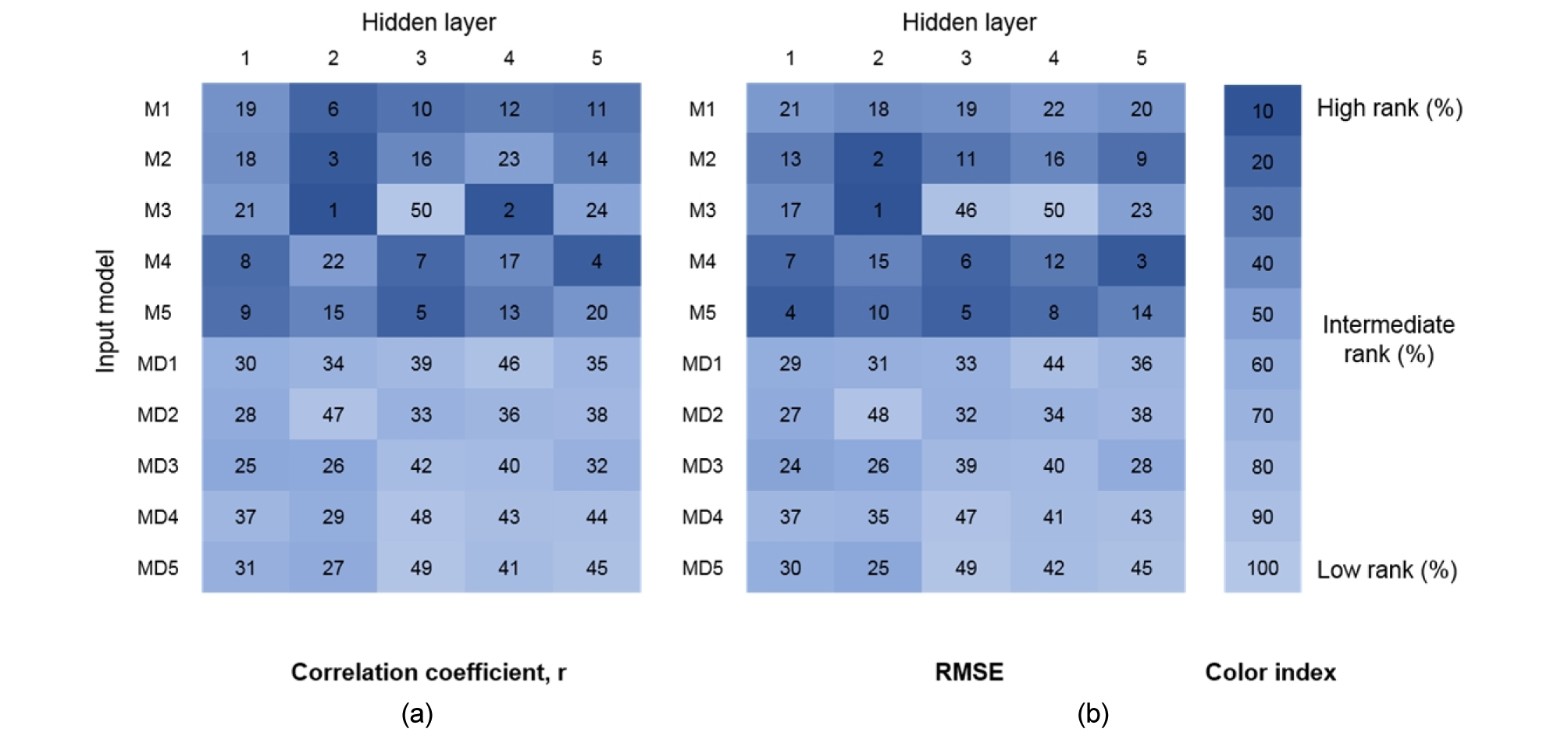
Fig. 7은 input model과 hidden layer에 따른 r과 RMSE의 값을 우수한 순서대로 순위를 매기고 순위대로 색을 입혀 도식화 한 결과를 보여준다. 색이 진할수록 예측결과의 신뢰성이 우수한 것을 나타내고 연한 색일수록 예측결과의 신뢰성이 비교적 떨어지는 것을 나타낸다. r과 RMSE 모두 대부분의 진한색이 M1 - M5에서 관찰된다. 또한, Fig. 7을 통하여 어떤 input 모델과 hidden layer가 가장 높은 신뢰성을 보이는지 쉽게 확인할 수 있다. 본 연구에서는 M3모델의 2 hidden layers (M3-2)가 r과 RMSE에서 모두 신뢰성이 가장 높은 것을 확인할 수 있다. MD1 - MD5 모델 중에서는 MD3모델의 1 hidden layer가 가장 높은 신뢰성을 보였다.

Fig. 7.

Graphical comparison of predicting performance with different input models and hidden layers. (a) correlation coefficient and (b) RMSE.

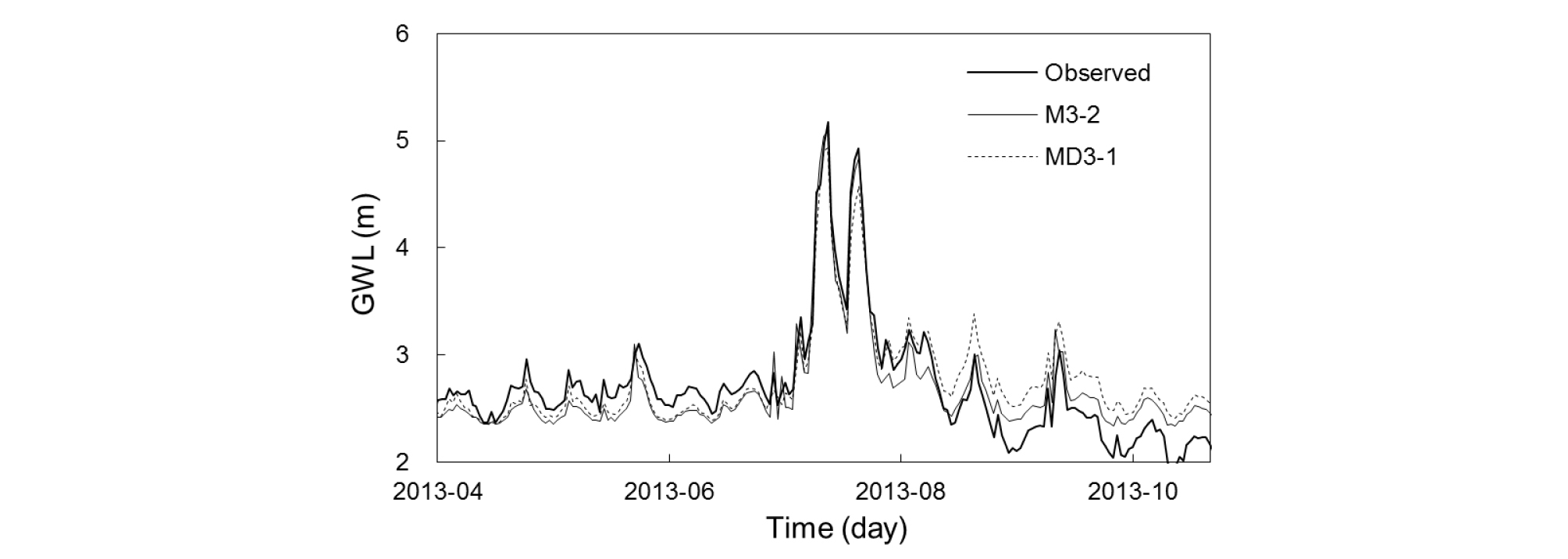
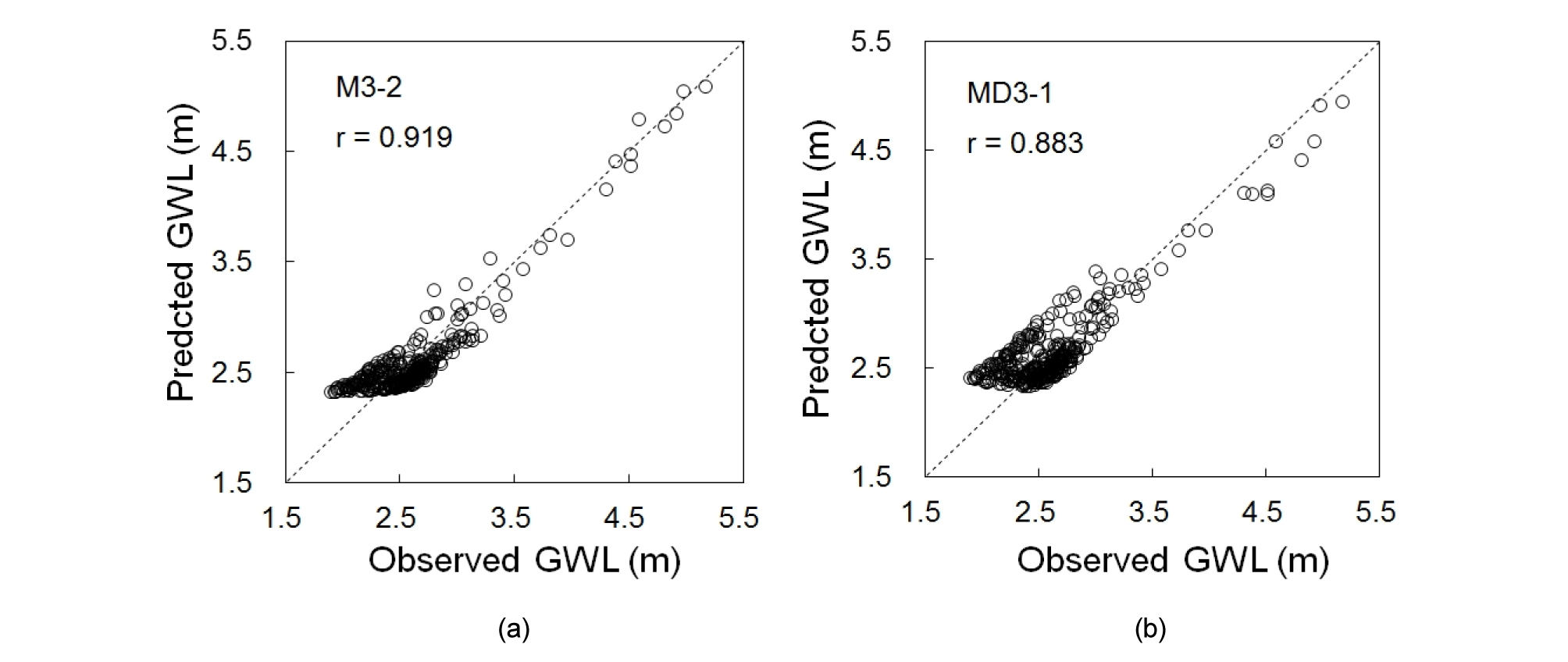
Fig. 8은 Dummy를 사용하지 않은 모델과 Dummy를 사용한 모델 중에서 가장 신뢰성이 높은 M3-2와 MD3-1의 예측결과를 관측 지하수위와 함께 보여준다. 두 모델 모두 관측 지하수위의 경향을 잘 예측하고 있으나, 8월 이후에 MD3-1이 M3-1보다 과대 예측하고 있는 것을 확인할 수 있다. Fig. 9는 Fig. 8의 관측 지하수위와 예측 지하수위를 산점도 (scatter plot)로 도시한 그림이다. M3-2의 포인트들이 Dummy를 input으로 추가한 MD3-1의 포인트들 보다 더욱 1:1라인에 집중되어 있는 것이 관찰되며. MD3-1의 결과는 포인트들이 더욱 산개되어 있는 것을 확인할 수 있다. 결론적으로, 연구 대상지역으로 선정한 서울시 마곡동은 ANN을 이용하여 지하수위를 예측할 경우 계절의 효과를 반영하기위에 제안된 Dummy를 인풋으로 사용하지 않는 것이 보다 우수한 예측신뢰성을 보인다.

Fig. 8.

Compared GWL observed and predicted using two input models.

Fig. 9.

Scatter plots. Input model (a) M3-2 and (b) MD3-1.

4. 결 론

지하수위는 기상 및 수문학적 요소들에 의하여 변동할 수 있으며, 이는 기초구조물의 지속적인 안정성과 사용성에 영향을 미칠 수 있다. 본 연구에서는 인공신경망 (ANN)을 이용하여 서울시 마곡동의 지하수위를 예측하였고, 지하수위 변동에 영향을 미칠 수 있는 인자로써 강우량, 하천수위, 기온을 input으로 사용하였다. 또한, 계절의 영향을 반영하기 위하여 제안된 Dummy를 추가하여 Dummy를 추가하지 않은 결과와 비교하였다.

본 연구 지역에서 ANN으로 지하수위를 예측할 경우, Dummy를 추가하지 않은 input 모델과 Dummy를 추가한 input 모델 모두 지하수위의 전반적인 변동을 잘 예측하였다.

계절의 영향을 반영하는 것으로 알려진 Dummy를 input으로 사용했을 경우, 오히려 사용하지 않은 경우보다 좋지 않은 예측 결과를 얻었다. 이는 input으로 들어가는 기온이 어느 정도 계절의 영향을 반영하고 있으며, 매월 마다 일괄적으로 값을 적용되는 형태의 Dummy는 강우가 여름철에 집중되는 연구 지역에서 오히려 예측 신뢰성을 떨어뜨리는 역할을 할 수 있다고 판단된다.

본 결과는 한 연구 대상지역에서 수행한 결과이므로 이를 일반화 하기에는 무리가 있으므로, 향후 수문, 지질 및 지형학적으로 의미가 있는 여러 지역을 대상으로 연구를 수행할 필요가 있다고 판단된다.